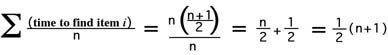Analysis of Algorithms

Analysis of Algorithms: An attempt to develop a means of measuring the efficiency of a piece of code. Basically, analysis of algorithms, attempts to measure the time it takes an algorithm to complete as a function of the size of its inputs. It is also a means of developing a formal proof that the algorithm works.

How does A of A work?

Consider the code fragment:

	for(i=0; i<n; i++)
		sum += i * i;

How fast does this code fragment run if n=10 relative to n=100 or n=1000 or n=1,000,000? The yardstick which is used to measure an algorithm's speed and efficiency as a function of the input size is called big O notation or just O notation. The list below shows the common measures used. They are listed from best to worst.


Common O Notation Measures
O(1)	Constant
O(log n)	Logarithmic
O(n)	Linear
O(n log n)	n log n
O(n²)	Quadratic
O(n³)	Cubic
O(2ⁿ)	Exponential
O(10ⁿ)	Exponential

If a function is analyzed and found to run in O(n²) time. Then it would take that function 100 times as long to run a sample of size 100 (100 x 100 = 10,000) as one of size 10 (10 x 10 = 100). Obviously, if an algorithm could be found that would do the same thing in O(n log n) or one of the lessor times, this would be a better algorithm to use.

A Simple Example

In a Sequential Search you are searching for a particular item (a key) in a list of n items. You must start at the first item in the list and search the items sequentially in the list until you find the one you are looking for. In the best case you would find the item on the first try, a measure of O(1). But, in the worst case the item would be the last one in the list.
The Average case would be: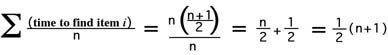

Now, to determine the O notation for this algorithm we look at the results of this calculation. We are looking for an O notation that is a whole multiple of n. Since we are not interested in absolute, but relative measures we can eliminate any constant multiple of the result. Thus, we can remove the 1/2 from the result of the above calculation giving O(n+1). Now for large values of n, one more makes no significant difference so we can also eliminate the constant 1. This give a final O notation for this algorithm of O(n).

There is another search algorithm which can be implemented if the list is in sorted order. That is the Binary Search. In a binary search you look first at the key for the item in the middle of the list. Even if this is not the item you are searching for you will know if the one you are searching for comes before or after this item, because the items are arranged in order. This means that immediately half of the items can be eliminated without having to search them directly. The search then continues by checking the middle item in the half that remains. A careful analysis of this algorithm shows it runs in O(log n).

Obviously O(log n) is better than O(n). The final decision as to which algorithm to use in a program must balance the improved search speed using the binary search as opposed to the increased time it takes to insert a new item into a list when the items must be kept in sequential order.