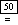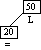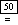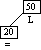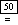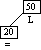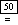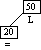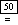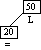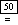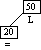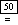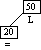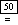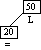A self-balancing AVL tree implemented in C++
Header file for an AVL tree
//==================================================================
// Code203_Tree.h
// Demonstration of an AVL tree which keeps the tree nodes in as
// near perfect balance as possible.
// Author: Dr. Rick Coleman
//==================================================================
#ifndef CODE203_TREE_H
#define CODE203_TREE_H
#include <iostream>
using namespace std;
struct AVLTreeNode
{
int key;
// Other data fields can be inserted here
AVLTreeNode *left;
AVLTreeNode *right;
AVLTreeNode *parent;
char balanceFactor;
};
class Code203_Tree
{
private:
AVLTreeNode *root;
public:
Code203_Tree(); // Constructor
~Code203_Tree(); // Destructor
void Insert(AVLTreeNode *n);
void restoreAVL(AVLTreeNode *ancestor, AVLTreeNode *newNode);
void adjustBalanceFactors(AVLTreeNode *end, AVLTreeNode *start);
void rotateLeft(AVLTreeNode *n);
void rotateRight(AVLTreeNode *n);
void adjustLeftRight(AVLTreeNode *end, AVLTreeNode *start);
void adjustRightLeft(AVLTreeNode *end, AVLTreeNode *start);
// void Delete(int key); // Not implemented yet
void PrintTree();
private:
void ClearTree(AVLTreeNode *n);
void Print(AVLTreeNode *n);
};
#endif
Implementation (.cpp) file for an AVL tree
//==================================================================
// Code203_Tree.cpp
// Demonstration of an AVL tree which keeps the tree nodes in as
// near perfect balance as possible.
// Author: Dr. Rick Coleman
// Date: January 2007
//==================================================================
#include "Code203_Tree.h"
using namespace std;
//------------------------------------------------------------------
// Default constructor
//------------------------------------------------------------------
Code203_Tree::Code203_Tree()
{
root = NULL; // Initialize root to NULL
}
//------------------------------------------------------------------
// Class destructor
//------------------------------------------------------------------
Code203_Tree::~Code203_Tree()
{
// Start recursive destruction of tree
ClearTree(root);
}
//------------------------------------------------------------------
// ClearTree()
// Recursively delete all node in the tree.
//------------------------------------------------------------------
void Code203_Tree::ClearTree(AVLTreeNode *n)
{
if(n != NULL)
{
ClearTree(n->left); // Recursively clear the left sub-tree
ClearTree(n->right); // Recursively clear the right sub-tree
delete n; // Delete this node
}
}
//------------------------------------------------------------------
// Insert()
// Insert a new node into the tree then restore the AVL property.
// Assumes that all three pointers (left, right, and parent) have
// already been set to NULL in the new node
//------------------------------------------------------------------
void Code203_Tree::Insert(AVLTreeNode *newNode)
{
AVLTreeNode *temp, *back, *ancestor;
temp = root;
back = NULL;
ancestor = NULL;
// Check for empty tree first
if(root == NULL)
{
root = newNode;
return;
}
// Tree is not empty so search for place to insert
while(temp != NULL) // Loop till temp falls out of the tree
{
back = temp;
// Mark ancestor that will be out of balance after
// this node is inserted
if(temp->balanceFactor != '=')
ancestor = temp;
if(newNode->key < temp->key)
temp = temp->left;
else
temp = temp->right;
}
// temp is now NULL
// back points to parent node to attach newNode to
// ancestor points to most recent out of balance ancestor
newNode->parent = back; // Set parent
if(newNode->key < back->key) // Insert at left
{
back->left = newNode;
}
else // Insert at right
{
back->right = newNode;
}
// Now call function to restore the tree's AVL property
restoreAVL(ancestor, newNode);
}
//------------------------------------------------------------------
// restoreAVL()
// Restore the AVL quality after inserting a new node.
// @param ancestor – most recent node back up the tree that is
// now out of balance.
// @param newNode– the newly inserted node.
//------------------------------------------------------------------
void Code203_Tree::restoreAVL(AVLTreeNode *ancestor, AVLTreeNode *newNode)
{
//--------------------------------------------------------------------------------
// Case 1: ancestor is NULL, i.e. balanceFactor of all ancestors' is '='
//--------------------------------------------------------------------------------
if(ancestor == NULL)
{
if(newNode->key < root->key) // newNode inserted to left of root
root->balanceFactor = 'L';
else
root->balanceFactor = 'R'; // newNode inserted to right of root
// Adjust the balanceFactor for all nodes from newNode back up to root
adjustBalanceFactors(root, newNode);
}
//--------------------------------------------------------------------------------
// Case 2: Insertion in opposite subtree of ancestor's balance factor, i.e.
// ancestor.balanceFactor = 'L' AND Insertion made in ancestor's right subtree
// OR
// ancestor.balanceFactor = 'R' AND Insertion made in ancestor's left subtree
//--------------------------------------------------------------------------------
else if(((ancestor->balanceFactor == 'L') && (newNode->key > ancestor->key)) ||
((ancestor->balanceFactor == 'R') && (newNode->key < ancestor->key)))
{
ancestor->balanceFactor = '=';
// Adjust the balanceFactor for all nodes from newNode back up to ancestor
adjustBalanceFactors(ancestor, newNode);
}
//--------------------------------------------------------------------------------
// Case 3: ancestor.balanceFactor = 'R' and the node inserted is
// in the right subtree of ancestor's right child
//--------------------------------------------------------------------------------
else if((ancestor->balanceFactor == 'R') && (newNode->key > ancestor->right->key))
{
ancestor->balanceFactor = '='; // Reset ancestor's balanceFactor
rotateLeft(ancestor); // Do single left rotation about ancestor
// Adjust the balanceFactor for all nodes from newNode back up to ancestor's parent
adjustBalanceFactors(ancestor->parent, newNode);
}
//--------------------------------------------------------------------------------
// Case 4: ancestor.balanceFactor is 'L' and the node inserted is
// in the left subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if((ancestor->balanceFactor == 'L') && (newNode->key < ancestor->left->key))
{
ancestor->balanceFactor = '='; // Reset ancestor's balanceFactor
rotateRight(ancestor); // Do single right rotation about ancestor
// Adjust the balanceFactor for all nodes from newNode back up to ancestor's parent
adjustBalanceFactors(ancestor->parent, newNode);
}
//--------------------------------------------------------------------------------
// Case 5: ancestor.balanceFactor is 'L' and the node inserted is
// in the right subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if((ancestor->balanceFactor == 'L') && (newNode->key > ancestor->left->key))
{
// Perform double right rotation (actually a left followed by a right)
rotateLeft(ancestor->left);
rotateRight(ancestor);
// Adjust the balanceFactor for all nodes from newNode back up to ancestor
adjustLeftRight(ancestor, newNode);
}
//--------------------------------------------------------------------------------
// Case 6: ancestor.balanceFactor is 'R' and the node inserted is
// in the left subtree of ancestor's right child
//--------------------------------------------------------------------------------
else
{
// Perform double left rotation (actually a right followed by a left)
rotateRight(ancestor->right);
rotateLeft(ancestor);
adjustRightLeft(ancestor, newNode);
}
}
//------------------------------------------------------------------
// Adjust the balance factor in all nodes from the inserted node's
// parent back up to but NOT including a designated end node.
// @param end– last node back up the tree that needs adjusting
// @param start – node just inserted
//------------------------------------------------------------------
void Code203_Tree::adjustBalanceFactors(AVLTreeNode *end, AVLTreeNode *start)
{
AVLTreeNode *temp = start->parent; // Set starting point at start's parent
while(temp != end)
{
if(start->key < temp->key)
temp->balanceFactor = 'L';
else
temp->balanceFactor = 'R';
temp = temp->parent;
} // end while
}
//------------------------------------------------------------------
// rotateLeft()
// Perform a single rotation left about n. This will rotate n's
// parent to become n's left child. Then n's left child will
// become the former parent's right child.
//------------------------------------------------------------------
void Code203_Tree::rotateLeft(AVLTreeNode *n)
{
AVLTreeNode *temp = n->right; //Hold pointer to n's right child
n->right = temp->left; // Move temp 's left child to right child of n
if(temp->left != NULL) // If the left child does exist
temp ->left->parent = n;// Reset the left child's parent
if(n->parent == NULL) // If n was the root
{
root = temp; // Make temp the new root
temp->parent = NULL; // Root has no parent
}
else if(n->parent->left == n) // If n was the left child of its' parent
n->parent->left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n->parent->right = temp;// Make temp the new right child
temp->left = n; // Move n to left child of temp
n->parent = temp; // Reset n's parent
}
//------------------------------------------------------------------
// rotateRight()
// Perform a single rotation right about n. This will rotate n's
// parent to become n's right child. Then n's right child will
// become the former parent's left child.
//------------------------------------------------------------------
void Code203_Tree::rotateRight(AVLTreeNode *n)
{
AVLTreeNode *temp = n->left; //Hold pointer to temp
n->left = temp->right; // Move temp's right child to left child of n
if(temp->right != NULL) // If the right child does exist
temp->right->parent = n;// Reset right child's parent
if(n->parent == NULL) // If n was root
{
root = temp; // Make temp the root
temp->parent = NULL; // Root has no parent
}
else if(n->parent->left == n) // If was the left child of its' parent
n->parent->left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n->parent->right = temp;// Make temp the new right child
temp->right = n; // Move n to right child of temp
n->parent = temp; // Reset n's parent
}
//------------------------------------------------------------------
// adjustLeftRight()
// @param end- last node back up the tree that needs adjusting
// @param start - node just inserted
//------------------------------------------------------------------
void Code203_Tree::adjustLeftRight(AVLTreeNode *end, AVLTreeNode *start)
{
if(end == root)
end->balanceFactor = '=';
else if(start->key < end->parent->key)
{
end->balanceFactor = 'R';
adjustBalanceFactors(end->parent->left, start);
}
else
{
end->balanceFactor = '=';
end->parent->left->balanceFactor = 'L';
adjustBalanceFactors(end, start);
}
}
//------------------------------------------------------------------
// adjustRightLeft
// @param end- last node back up the tree that needs adjusting
// @param start - node just inserted
//------------------------------------------------------------------
void Code203_Tree::adjustRightLeft(AVLTreeNode *end, AVLTreeNode *start)
{
if(end == root)
end->balanceFactor = '=';
else if(start->key > end->parent->key)
{
end->balanceFactor = 'L';
adjustBalanceFactors(end->parent->right, start);
}
else
{
end->balanceFactor = '=';
end->parent->right->balanceFactor = 'R';
adjustBalanceFactors(end, start);
}
}
//------------------------------------------------------------------
// PrintTree()
// Intiate a recursive traversal to print the tree
//------------------------------------------------------------------
void Code203_Tree::PrintTree()
{
cout << "\nPrinting the tree...\n";
cout << "Root Node: " << root->key << " balanceFactor is " <<
root->balanceFactor << "\n\n";
Print(root);
}
//------------------------------------------------------------------
// Print()
// Perform a recursive traversal to print the tree
//------------------------------------------------------------------
void Code203_Tree::Print(AVLTreeNode *n)
{
if(n != NULL)
{
cout<<"Node: " << n->key << " balanceFactor is " <<
n->balanceFactor << "\n";
if(n->left != NULL)
{
cout<<"\t moving left\n";
Print(n->left);
cout<<"Returning to Node" << n->key << " from its' left subtree\n";
}
else
{
cout<<"\t left subtree is empty\n";
}
cout<<"Node: " << n->key << " balanceFactor is " <<
n->balanceFactor << "\n";
if(n->right != NULL)
{
cout<<"\t moving right\n";
Print(n->right);
cout<<"Returning to Node" << n->key << " from its' right subtree\n";
}
else
{
cout<<"\t right subtree is empty\n";
}
}
}
Main file used to test the AVL tree
//==================================================================
// AVLTreeMain.cpp
// Demonstration of an AVL tree which keeps the tree nodes in as
// near perfect balance as possible.
// Author: Dr. Rick Coleman
// Date: January 2007
//==================================================================
#include "Code203_Tree.h"
#include <iostream>
using namespace std;
AVLTreeNode *createNewNode(int key);
int main()
{
Code203_Tree *theAVLTree;
char ans[32];
cout << "Ready to test AVL trees. Press Enter to start.\n\n";
gets(ans);
// Test each case by adding some nodes to the tree then
// printing the tree after each insertion
// Create a tree and test case 1
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 1\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20 to trigger test of Case 1 to left. Root is ancester.\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90 to trigger test of Case 1 to right. Root is ancester.\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 1\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 2
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 2\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20. Ancester's balance factor changes to L\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70 to trigger test of Case 2. Ancester's balance factor changes to =\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90. Ancester's balance factor changes to R.\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
// Add 15
cout << "\nAdding Node 15 to trigger test of Case 2. Ancesters balance factor changes to =\n";
theAVLTree->Insert(createNewNode(15));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 2\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 3a
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 3a\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 60
cout << "\nAdding Node 60\n";
theAVLTree->Insert(createNewNode(60));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
// Add 95
cout << "\nAdding Node 95 to trigger test of case 3.\n";
theAVLTree->Insert(createNewNode(95));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 3a\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 3b
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 3b\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 60
cout << "\nAdding Node 60\n";
theAVLTree->Insert(createNewNode(60));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
// Add 75
cout << "\nAdding Node 75 to trigger test of case 3.\n";
theAVLTree->Insert(createNewNode(75));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 3b\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 4
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 4a\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 30
cout << "\nAdding Node 30\n";
theAVLTree->Insert(createNewNode(30));
theAVLTree->PrintTree();
// Add 15
cout << "\nAdding Node 15\n";
theAVLTree->Insert(createNewNode(15));
theAVLTree->PrintTree();
// Add 10
cout << "\nAdding Node 10 to trigger test of case 4.\n";
theAVLTree->Insert(createNewNode(10));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 4a\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 4
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 4b\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 30
cout << "\nAdding Node 30\n";
theAVLTree->Insert(createNewNode(30));
theAVLTree->PrintTree();
// Add 15
cout << "\nAdding Node 15\n";
theAVLTree->Insert(createNewNode(15));
theAVLTree->PrintTree();
// Add 10
cout << "\nAdding Node 17 to trigger test of case 4.\n";
theAVLTree->Insert(createNewNode(17));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 4b\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 5
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 5a\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 10
cout << "\nAdding Node 15\n";
theAVLTree->Insert(createNewNode(15));
theAVLTree->PrintTree();
// Add 30
cout << "\nAdding Node 30\n";
theAVLTree->Insert(createNewNode(30));
theAVLTree->PrintTree();
// Add 25
cout << "\nAdding Node 25 to trigger test of case 5.\n";
theAVLTree->Insert(createNewNode(25));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 5a\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 5
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 5b\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 10
cout << "\nAdding Node 15\n";
theAVLTree->Insert(createNewNode(15));
theAVLTree->PrintTree();
// Add 30
cout << "\nAdding Node 30\n";
theAVLTree->Insert(createNewNode(30));
theAVLTree->PrintTree();
// Add 35
cout << "\nAdding Node 35 to trigger test of case 5.\n";
theAVLTree->Insert(createNewNode(35));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 5b\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 6
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 6a\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 60
cout << "\nAdding Node 60\n";
theAVLTree->Insert(createNewNode(60));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
cout<< "\n***** Adding Node to trigger test of case 6\n";
// Add 55
cout << "\nAdding Node 55\n";
theAVLTree->Insert(createNewNode(55));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 6a\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nPress Enter to start the next test.\n\n";
gets(ans);
// Create a tree and test case 6
theAVLTree = new Code203_Tree();
cout<< "-----------------------------------------------\n";
cout<< "TESTING CASE 6b\n\n";
// Add 50
cout << "\nAdding Node 50\n";
theAVLTree->Insert(createNewNode(50));
theAVLTree->PrintTree();
// Add 20
cout << "\nAdding Node 20\n";
theAVLTree->Insert(createNewNode(20));
theAVLTree->PrintTree();
// Add 70
cout << "\nAdding Node 70\n";
theAVLTree->Insert(createNewNode(70));
theAVLTree->PrintTree();
// Add 60
cout << "\nAdding Node 60\n";
theAVLTree->Insert(createNewNode(60));
theAVLTree->PrintTree();
// Add 90
cout << "\nAdding Node 90\n";
theAVLTree->Insert(createNewNode(90));
theAVLTree->PrintTree();
cout<< "\n***** Adding Node to trigger test of case 6\n";
// Add 65
cout << "\nAdding Node 65\n";
theAVLTree->Insert(createNewNode(65));
theAVLTree->PrintTree();
cout<< "\nEND TESTING CASE 6b\n\n";
delete theAVLTree;
cout<< "-----------------------------------------------\n";
cout<< "-----------------------------------------------\n";
cout << "\nAll testing complete.\n";
cout << "\nPress Enter to terminate the application.\n\n";
gets(ans);}
//---------------------------------------------
// Create a new tree node with the given key
//---------------------------------------------
AVLTreeNode *createNewNode(int key)
{
AVLTreeNode *temp = new AVLTreeNode();
temp->key = key;
temp->left = NULL;
temp->right = NULL;
temp->parent = NULL;
temp->balanceFactor = '=';
return temp;
}
Results from Testing the AVL Tree
Below is a series of images illustrating the state of the tree after
inserting nodes in the order given in AVLTreeMain.cpp. Note the effects
when the key node is inserted in each of the six cases. The first diagram
shows the appearance of the tree after the key node is added and before the
rotations are applied. The second diagram shows how the tree looks after
the rotations and adjustments to the balanceFactor in each node have been
applied.
|
|
|
|
|
|
Testing Case 1 - Ancestor is NULL, i.e. balanceFactor is '=' in
all of the predecessors
|
Step 1a
Inserting Node 50
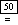
|
Step 2a
Inserting Node 20
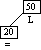
Simple Case 1: Balance factor
of ancestor 50 adjusted.
|
Step 3a
Inserting Node 70
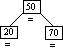
|
Step 4a
Inserting Node 30
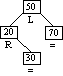
Case 1: Balance factors of
ancestors 20 and 50 adjusted.
|
Step 1b
Inserting Node 50
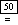
|
Step 2b
Inserting Node 20
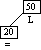
Simple Case 1: Balance factor
of ancestor 50 adjusted.
|
Step 3b
Inserting Node 70

|
Step 4b
Inserting Node 90
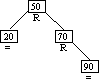
Case 1: Balance factors of
ancestors 70 and 50 adjusted.
|
|
|
|
|
|
|
|
Testing Case 2 - Insertion made in the opposite subtree of
the ancestor's balance factor, i.e. ancestor.balanceFactor = 'L' and
insertion made in ancestor's right subtree, OR ancestor.balanceFactor = 'R'
and insertion made in ancestor's left subtree
|
Step 1a
Inserting Node 50
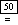
|
Step 2a
Inserting Node 20
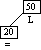
|
Step 3a
Inserting Node 70

Case 2: Ancestor balance factor was L
insertion made in right sub-tree.
Ancestor's balance factor adjusted.
|
|
|
Step 1b
Inserting Node 50
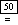
|
Step 2b
Inserting Node 20
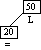
|
Step 3b
Inserting Node 70

|
Step 4b
Inserting Node 90

|
Step 5b
Inserting Node 15
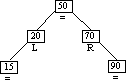
Case 2: Ancestor balance factor was R
insertion made in left sub-tree.
Ancestor's balance factor adjusted.
|
|
|
|
|
|
|
|
Testing Case 3 - Ancestor.balanceFactor = 'R' and node inserted is
in the right subtree of ancestor's right child.
|
|
These 5 steps are common to both Case3a and Case3b.
|
Step 1
Inserting Node 50
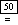
|
Step 2
Inserting Node 20
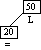
|
Step 3
Inserting Node 70

|
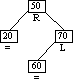
Step 4
Inserting Node 60
|
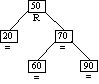
Step 5
Inserting Node 90
|
|
Case3a:
|
|
Case3b:
|
Step 6a
Inserting Node 95
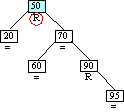
|
Case 3 triggered
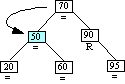
Case 3: Ancestor balance factor was R
insertion made in right sub-tree of ancestor's.
right child.
Single left rotation of ancestor.
|
|
Step 6B
Inserting Node 75
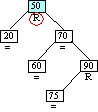
|
Case 3 triggered
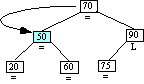
Case 3: Ancestor balance factor was R
insertion made in right sub-tree of ancestor's.
right child.
Single left rotation of ancestor.
|
|
|
|
|
|
|
|
Testing Case 4 - Ancestor.balanceFactor = 'L' and node inserted is
in the left subtree of ancestor's left child.
|
|
These 5 steps are common to both Case4a and Case4b.
|
Step 1
Inserting Node 50
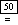
|
Step 2
Inserting Node 20
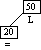
|
Step 3
Inserting Node 70

|
Step 4
Inserting Node 30
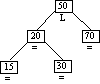
|
Step 5
Inserting Node 15
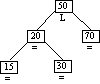
|
|
Case4a:
|
|
Case4b:
|
Step 6a
Inserting Node 10
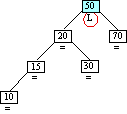
|
Case 4 triggered
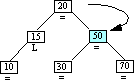
Case 4: Ancestor balance factor was L
insertion made in left sub-tree of ancestor's.
left child.
Single right rotation of ancestor.
|
|
Step 6B
Inserting Node 17
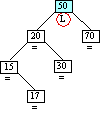
|
Case 4 triggered
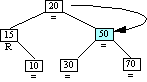
Case 4: Ancestor balance factor was L
insertion made in left sub-tree of ancestor's.
left child.
Single right rotation of ancestor.
|
|
|
|
|
|
|
|
Testing Case 5 - Ancestor.balanceFactor = 'L' and node inserted is
in the right subtree of ancestor's left child.
|
|
These 5 steps are common to both Case5a and Case5b.
|
Step 1
Inserting Node 50
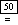
|
Step 2
Inserting Node 20
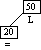
|
Step 3
Inserting Node 70

|
Step 4
Inserting Node 30

|
Step 5
Inserting Node 15

|
|
Case5a:
|
Step 6a
Inserting Node 25
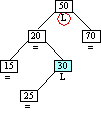
|
|
Case 5 triggered
Ancestor balance factor was L
insertion made in right sub-tree
of ancestor's left child.
Double right rotation of right child
of ancestor's left child.
|
Case 5-Step 1
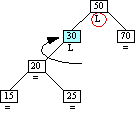
|
Case 5-Step 2
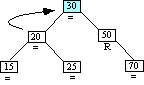
|
|
Case5b:
|
Step 6b
Inserting Node 35
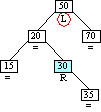
|
|
Case 5 triggered
Ancestor balance factor was L
insertion made in right sub-tree
of ancestor's left child.
Double right rotation of right child
of ancestor's left child.
|
Case 5-Step 1
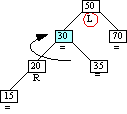
|
Case 5-Step 2
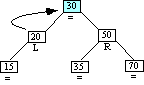
|
|
|
|
|
|
|
|
Testing Case 6 - Ancestor.balanceFactor = 'R' and node inserted is
in the left subtree of ancestor's right child.
|
|
These 5 steps are common to both Case6a and Case6b.
|
Step 1
Inserting Node 50
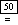
|
Step 2
Inserting Node 20
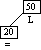
|
Step 3
Inserting Node 70

|
Step 4
Inserting Node 30

|
Step 5
Inserting Node 15

|
|
Case6a:
|
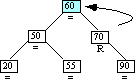
Step 6a
Inserting Node 55
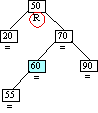
|
|
Case 6 triggered
Case 6: Ancestor balance factor was R
insertion made in left sub-tree
of ancestor's right child.
Double left rotation of left child
of ancestor's right child.
|
Case 6-Step 1
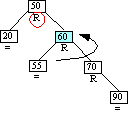
|
Case 6-Step 2
|
|
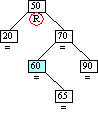
Case6b:
|
Step 6a
Inserting Node 65
|
|
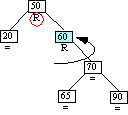
Case 6 triggered
Case 6: Ancestor balance factor was R
insertion made in left sub-tree
of ancestor's right child.
Double left rotation of left child
of ancestor's right child.
|
Case 6-Step 1
|
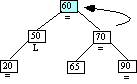
Case 6-Step 2
|
|
|