Recursion

Functions Calling Themselves

What is Recursion?

Recursion is simply the ability of a function to be able to call itself.

Recursion is a technique of problem solving by breaking a large problem down into successively smaller versions of itself.

A humorous example


Problem: How do you eat an elephant?
Recursive solution: You eat one bite. Then you eat the rest of the elephant.
And how do you eat the rest of the elephant? You eat another bite, then you eat what is left. And, so on until the elephant is completely consumed.


A programming example

Problem: How do you find the sum of squares of all numbers between some starting integer m and some ending integer n?
Iterative solution: A simple iterative solution, without using recursion, is just to loop over all numbers from m to n and add up the squares of all the numbers. The following code illustrates this.
     int SumOfSquares(int m, int n)
     {
          int i, sum;
          for(i = 0; i <= n; i++)
               sum += i*i;
          return sum;
     }


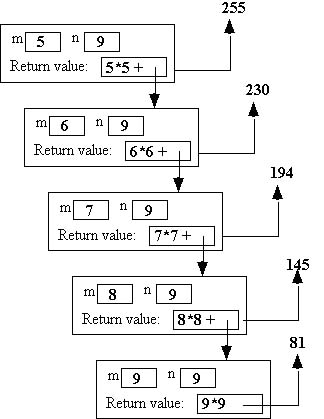
Recursive solution: In this recursive example if m is not equal to n then the function returns the square of m plus whatever is returned by the recursive call to the same function passing in m+1 and n as arguments. The following code illustrates this.
     int SumOfSquares(int m, int n)
     {
          if(m < n)
               return m*m + SumOfSquares(m+1, n);  // Recursive call
          else
               return m*m;
     }


Note that as long as SumOfSquares() is called with m not equal to n we make a recursive call to the same function but passing in a slightly smaller version of the same problem (m+1 and n). When m is equal to n we call this the base case and just return m*m without a recursive call.

It is also possible to solve this problem recursively by decrementing n instead of incrementing m. 
     int SumOfSquares(int m, int n)
     {
          if(m < n)
               return SumOfSquares(m, n-1) + n*n;  // Recursive call
          else
               return n*n;
     }


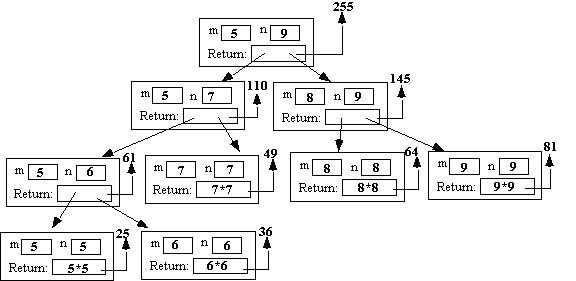
And if you just want to show off you can solve this problem a third way by using a solution that divides the problem into two halves and solves each half problem
     int SumOfSquares(int m, int n)
     {
          int middle;

          if(m == n)
               return m*m;  // Base call
          else
          {
               middle = (m+n)/2;   // Note: this is integer division
               return SumOfSquares(m, middle) + SumOfSquares(middle+1, n);
          }
     }


Important Definitions

Base case -- The case for which the solution can be stated nonrecursively. In the SumOfSquares example the base case is when m equals n. The sum of squares of a single number is the number squared.

General (recursive) case -- The case for which the solution to a problem is expressed in terms of a smaller versin of itself. For example, the sum of squares of the numbers from m to n can be stated as m2 plus the results of the smaller problem of the sum of squares from m+1 to n.

How do you determine if there is a recursive solution to a problem?

  1. Base case question
    Is there a base case? Is there a way out of the function that does not require a recursive call and in which the function works correctly. For example, the sum of squares problem has a base case when m==n.

  2. Smaller caller question
    Does each recursive call result in a smaller version of the original problem which leads inescapably to the base case. For example the sum of squares recursive calls always are for (m+1, n). If (m < n) to start with then these recursive calls eventually lead to a call in which m == n, the base case.

  3. General case question
    Assuming each recursive call works correctly, does this lead to the correct solution to the whole problem?
    The answer to this question can be shown through induction:

    1. Show that the solution works for the base case, i.e. SumOfSquares(n, n).
    2. Assume that the solution works for the case of SumOfSquares(n, n+1).
    3. Now to finish the proof show that the solution works for SumOfSquares(n, n+2):
      1. The return value from the first recursive call to the function would be n2 + SumOfSquares(n+1, n+2).
      2. This is just the results of a call to the base case SumOfSquares(n, n) which we have already shown to work, and a call to what is syntatically equivalent to SumOfSquares(n, n+1) which we have assumed works.
      3. Thus, by induction, we have shown that the function works for all values of m and n where m < n.

An internal look at recursive calls.

When you call a function in a program the operating system creates a special data structure called a Call Frame and pushes it onto a special abstract data type called the Call Stack.




The call frame contains, among other things, the address in memory where execution will return to when the function is exited, the arguments passed into the function, and the value returned by the function.

Example 1 with m incrementing

Look at the illustration below to see what is happening when the call to the first SumOfSquares(m, n) function is made. In this example the value of m is incremented in each recursive call.
  1. First call gets 5 and 9 as arguments. It will return to the original caller 5*5 + SumOfSquares(6, 9).
  2. Second call gets 6 and 9 as arguments. It will return to the first call 6*6 + SumOfSquares(7, 9).
  3. Third call gets 7 and 9 as arguments. It will return to the second call 7*7 + SumOfSquares(8, 9).
  4. Fourth call gets 8 and 9 as arguments. It will return to the third call 8*8 + SumOfSquares(9, 9).
  5. Fifth call gets 9 and 9 as arguments. Since this is now the base case it will return to the fourth caller 9*9.



Example 2 with n decrementing

Look at the illustration below to see what is happening when the call to the second SumOfSquares(m, n) function is made. In this example the value of n is decremented in each recursive call.
  1. First call gets 5 and 9 as arguments. It will return to the original caller SumOfSquares(5, 8) + 9*9.
  2. Second call gets 5 and 8 as arguments. It will return to the first caller SumOfSquares(5, 7) + 8*8.
  3. Third call gets 5 and 7 as arguments. It will return to the second caller SumOfSquares(5, 6) + 7*7.
  4. Fourth call gets 5 and 6 as arguments. It will return to the third caller SumOfSquares(5, 5) + 6*6.
  5. Fifth call gets 5 and 5 as arguments. Since this is now the base case it will return to the fourth caller 5*5.



Example 3 with the range m to n halved each call

Look at the illustration below to see what is happening when the call to the third SumOfSquares(m, n) function is made. This example is a little more complex because in each function call there are two recursive calls. The first recursive call is for the first half of the argument range and the second recursive call is for the second half of the argument range.
  1. First call gets 5 and 9 as arguments from the original caller. It will divide the argument range into (5, 7) and (8, 9) and return to the original caller SumOfSquares(5, 7) + SumOfSquares(8, 9).
  2. Second call gets 5 and 7 as arguments from the first caller. It will divide the argument range into (5, 6) and (7, 7) and return to the first caller SumOfSquares(5, 6) + SumOfSquares(7, 7).
  3. Third call gets 5 and 6 as arguments from the second caller. It will divide the argument range into (5, 5) and (6, 6) and return to the second caller SumOfSquares(5, 5) + SumOfSquares(6, 6).
  4. Fourth call gets 5 and 5 as arguments from the third caller. Since this is now a base case it will return to the third caller 5*5.
  5. Fifth call gets 6 and 6 as arguments from the third caller. Since this is now a base case it will return to the third caller 6*6.
  6. Sixth call gets 7 and 7 as arguments from the second caller. Since this is now a base case it will return to the second caller 7*7.
  7. Seventh call gets 8 and 9 as arguments from the first caller. It will divide the argument range into (8, 8) and (9, 9) and return to the first caller SumOfSquares(8, 8) + SumOfSquares(9, 9).
  8. Eighth call gets 8 and 8 as arguments from the seventh caller. Since this is now a base case it will return to the seventh caller 8*8.
  9. Ninth call gets 9 and 9 as arguments from the seventh caller. Since this is now a base case it will return to the seventh caller 9*9.



Another example using ADTs.
Reversing the order of nodes in a linked list

Problem: You are given a linked list such as the one shown in the first illustration below.



The problem is to reverse all the nodes in the list so that the new list looks like the one in this second illustration.



This problem could also be solved in one of three ways just like the SumOfSquares problem. Let's look at the approach that parallels the first of the SumOfSquares solutions. In this solution we will use the following approach:
  1. Remove the first node from the list.
  2. Reverse the order of the rest of the list.
  3. Concatenate the first node to the end of the reversed rest of the list.

In order to solve this problem we will need three functions. In each assume we have defined a data structure called NodeType which contains a key value, some other data, and a next pointer.
  1. NodeType *Reverse(NodeType *List) -- The main function to do the reversing. It is from this function that the recursive call will be made. It takes a single argument, a pointer to the list to be reversed.
  2. void Partition(NodeType *Lst, NodeType **Hd, NodeType **Tl) -- This function handles partitioning a list into its' first node and the rest of the list. Note the use of handles (**Hd and **Tl). These are pointers to pointers. This means if we pass the address of a pointer (a pointer to the pointer) into a function we can change what the original pointer is pointing to by changing the address stored there.
  3. NodeType *Concat(NodeType *L1, NodeType *L2) -- This function will reconnect the former head of a list to the tail of a reversed list. 
NodeType *Reverse(NodeType *List)
{
    NodeType *Head;
    NodeType *Tail;
    NodeType *RList;
    if(List == NULL)    // Base Case - the empty list 
        return (NULL);
    else
    {
        Partition(List, &Head, &Tail); // Note we are passing pointers to Head and Tail, that is Handles
        RList = Concat(Reverse(Tail), Head);
        return (RList);
    }
}

void Partition(NodeType *Lst, NodeType **Hd, NodeType **Tl)
{
    if(Lst != NULL)
    {
        *Tl = Lst->next;      // By using a handle we are actually changing what Tail in Reverse() is pointing to.
        *Hd = Lst;            // This will set Head in Reverse() pointing to the rest of the list
        (*Hd)->next = NULL;   // This will set the next pointer in the node Head, in Reverse(), pointing to NULL
    }                         // Note the use of parentheses due to binding of *
}

NodeType *Concat(Nodetype *L1, Nodetype *L2)
{                          // L1 = reversed tail of a list, L2 = head of a list
    NodeType *temp;        // A search pointer used to find the end of list L1

    if(L1 == NULL)
        return (L2);    // This is L2 concated to a NULL list
    else
    {
        temp =  L1;    
        while(temp->next != NULL)
            temp = temp->next;   // Search for end of list L1
        temp->next = L2;         // Concatenate L2 to end of L1
        return L1;
    }
}


Are you beginning to get the idea behind recursion?

Deciding when to use recursion.

How do you decide if you can use recursion to solve a problem? Consider the following four points in determining if recursion is a valid solution.
  1. Make sure you have an exact definition of the problem. You must have this to determine if the solution can be a recursive one.
  2. Determine the size of the problem. If may be too big to solve recursively. A problem like SumOfSquares(1, 999999999) just might exceed the call stack memory of your computer.
  3. Identify the base case. If there is a base case you can answer "yes" to the Base case question.
  4. Identify the general case. If there is one (or more) you can answer "yes" to the Smaller caller question and the General case question.


Dangers in using recursion

There are certain dangers you must be aware of when using recursion.
  1. Infinite regression. This occurs when there is no base case or there is no allowance for one.
    Consider the following example of a recursive function to calculate factorials. 
                int Factorial(int N)
            {
                if(N == 1)
                    return N;
                else
                    return (N * Factorial(N-1);
            }
    This function works fine except for certain situations. What would happen if this function were called with Factorial(0) or Factorial(-1). This will continue infinitely until memory for call frames is used up or the integer finally cycles around to the positive and then finally reduces to 1. In other words there is an arithmetic underflow error when calculating (-MAXINT - 1).

  2. Ranges out of bounds of the machine capability and not checking just how much computation there is involved in what you want to do recursively. What would happen if you called SumOfSquares(1, 999999999)?

  3. Private recursive functions in classes. In many cases you may need a recursive function in a class, but the function must take as an argument a private member variable of the class. In this case there is no way you can correctly call the function, even if it is public, because you can't access the private member variable. For example, suppose you needed the list reversing function in a linked list class, but you can't call it because it requires the first call to pass in the pointer to the head of the list which is private. The solution is to have a public function which can be called without arguments and it then calls the private function with the head pointer argument.
    private:
    Node *head; // Private pointer to head of list
    Node *Reverse(Node *Hd); // Private function which can access the head pointer

    public:
    void ReverseIt(); // Public function to be called to start the recursion

    The ReverseIt() function would be implemented like this:

    		void ListClass::ReverseIt()
		{
		    Reverse(head);
		}