Heap Sort
Sort Type: Comparison-Based Sorting / Priority Queue Sorting
Algorithm
Description:
All Priority Queue Sorting is based on arranging the data structures into a priority queue
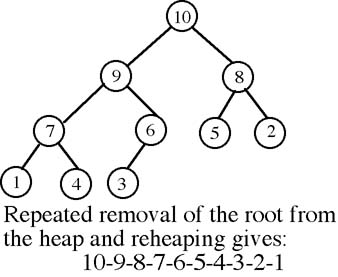
using the keys. Because of its structure a Heap is automatically a priority queue. Repeatedly
dequeuing structures from the heap and moving them into an array will give a sorted array.
Data holder: Heap of data structures and an empty array of data structures.
Technique:
-
Build a heap from the given data.
-
Copy the data in the root node of the heap (it will be the one with the
largest key or greatest priority) and place it at the end of the sorted
data (assuming the sorted array is filled from right to left).
-
Reheap the heap.
-
Repeat until the heap is empty.
Analysis:
At first, it would seem that because of the shifting and re-building of the
heap that this sort would take as long, or longer, than Selection Sort.
Surprisingly this sort can run in O(n log n).
