figure 1
Basic Shortest Path Algorithm |
|||
| Set a flag in all vertices to "UNSEEN" | |||
| Pick a starting vertex and mark it as "IN TREE" | |||
| Mark all vertices adjacent to the start vertex as "FRINGE" | |||
| Loop while there are vertices in the graph not marked as "IN TREE" | |||
| Find the vertex in the fringe at a minimum distance from the start vertex. | |||
| Add that vertex to the tree and mark it as "IN TREE" | |||
| For each vertex adjacent to this vertex | |||
|
Set the state of the adjacent vertex to "FRINGE" Calculate its' distance from the starting vertex Set the shortest distance to each node in the fringe |
|||
| end loop | |||
| Return Shortest Distance | |||

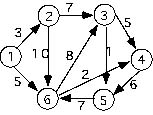
If we are searching for the shortest path from node 1 to any other given node in the graph we need to look at all the possible paths from node 1 to node w and pick the shortest. Listing all the possible paths from node 1 to the other nodes with their lengths gives:
Paths to 1: 1-->1 (0) Paths to 2: 1-->2 (3) Paths to 3: 1-->2-->3 (10), 1-->6-->3 (13) Paths to 4: 1-->2-->3-->4 (15), 1-->6-->4 (7), 1-->6-->3-->4 (18) Paths to 5: 1-->2-->3-->4-->5 (21), 1-->2-->3-->5 (11) 1-->2-->6-->3-->4-->5 (32), 1-->2-->6-->4-->5 (21), 1-->6-->4-->5 (13), 1-->6-->3-->5 (14) Paths to 6: 1-->6 (5), 1-->2-->6 (13), 1-->2-->3-->5-->6 (22), 1-->2-->3-->4-->5-->6 (38)
You can go through this list and pick the shortest path from all the possible paths to each node. We can build a diagram which would give us the shortest paths. To do this we will rebuild the graph diagram into a tree (see figure 6). At any point in the building of the tree the nodes in the graph will be classified in one of three categories: (1) "intree"--those nodes which have already been added to the tree, (2) "fringe" -- those nodes which are immediately adjacent to any of the nodes in the tree, (3) "unseen" -- all remaining nodes.
As an example let's trace the paths from node 1 to node 5. Beginning with node 1 as the starting point we see that there are two nodes in the fringe {2,6}and three nodes unseen {3,4,5}. With no additional information the path to node 2 and the path to node 6 represent the current shortest path to each. This gives us a tree as shown in Figure 2.
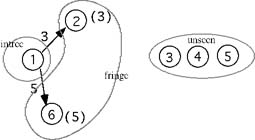
We select node 2 first, because it is the closest to 1 of all the nodes in the fringe. Adding it to the tree and updating the fringe we get the tree in figure 3. Note that node 6 is in the fringe for node 2 but the path to node 6 via node 2 is longer than the direct path from node 1 to node 6 so we don't consider path 1-->2-->6 as acceptable.
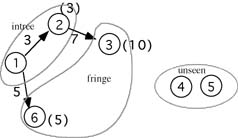
Of the two nodes in the fringe now, node 6 is closest so it is added to the tree and all the nodes adjacent to 6 are moved into the fringe. This gives figure 4.
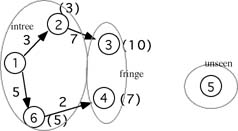
Node 4 is now the closest to node 1 of all the nodes in the fringe so it is selected and the nodes adjacent to it added to the fringe. This gives the tree shown in figure 5.
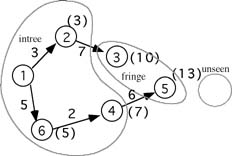
Next we add node 3 to the tree since it is the closest to node 1. This will also reveal another path to node 5, 1-->2-->3-->5 = 11 which is shorter than the current path length of 13 so 11 is substituted for 13. Node 3 is added to the tree. This leaves only node 5 in the fringe. After it is added to the tree we get a final tree as shown in figure 6.
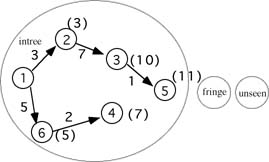
The shortest path from node 1 to node 5, then is the path 1-->2-->3-->5. How can we implement this approach to solving the problem of Dijkstra's algorithm? To keep things simple we will implement all of our abstract data types as arrays of structures. The graph will be represented as an adjacency set, which uses two data structures, Link and Node.
typedef struct linktype
{
int link; /* Node linked to */
int weight; /* Weight of the link */
} Link;
typedef struct nodetype
{
int data; /* In this example, just the node number. */
Link links[5]; /* A small array for demo only */
}Node;
A diagram of the arrays representing the graph adjacency list is shown in Figure 7.

Below is pseudocode for Dijkstra's Algorithm modified from that in the text to make it clearer. Note that in many places the index into an array is given as [x-1]. This is because the array elements are numbered 0..(n-1) while the nodes are numbered 0..n.
#define MAXVERTICES 6 // only for this example
#define MAXLINKS 5 // only for this example
#define Minimum(X,Y) ((X) < (Y)) ? (X) : (Y)
typdef enum{intree, fringe, unseen} StatusType;
Define an array of type Node.
Insert all data in the array to build the graph.
Input start (v) and end (w) node numbers from user
Call ShortestPath(AdjacencyList, 6, v, w)
int ShortestPath(Node AdjacencyList[], int n, int v, int w)
// AdjacencyList -- adjacency list of nodes in graph
// n -- number of nodes in the graph (MAXVERTICES)
// v -- number of the starting vertex (1..MAXVERTICES)
// w -- number of the destination vertex (1..MAXVERTICES)
int ShortestDist[MAXVERTICES];
int W[MAXVERTICES];
StatusType status[MAXVERTICES];
// -------------------- INITIALIZATION SECTION --------------------
Initialize tree array W to empty.
Initialize ShortestDist array to all maximum.
Initialize status array to all unseen.
// --------------------------- SETUP SECTION ---------------------------
Add node v to W array
Set shortest distance from v to v = 0
Set status of v to intree
For each node adjacent to v
Set status to fringe
Set shortest distance to weight of link from v
// ----------------------- MAIN LOOP SECTION -----------------------
// Repeatedly enlarge W until it includes all vertices in the graph
while(there are nodes in the graph not in W)
Find node n, among those in the fringe, at the minimum distance from v
Add node n to W array
Set status of node n to intree
For each node adjacent to node n
Set status of adjacent node to fringe
Calculate distance D from v to adjacent node through node n, i.e.
shortest distance to n + distance from n to adjacent node.
Set shortest distance to the adjacent node to
Minimum(D, ShortestDist[adjacent node])
end while
return ShortestDist[node w]
end ShortestPath function
FYI. This algorithm runs in O(n2).
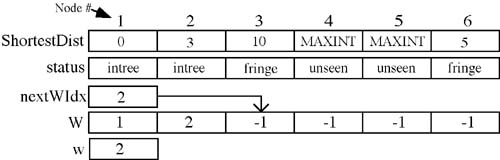
Let us now trace this algorithm using the graph given above. To start we declare and initialize a number of variables. We will use an array of integers called ShortestDist to hold the shortest distances to each node as it is encountered. This array is initialized to a very large number. In some systems this is a #defined constant known as MAXINT. In order to keep up with which vertices have been encountered and added to the list, referred to in the text as W, we will maintain the status of each node as {intree, fringe, unseen} using the previously described enumerated data type. We will use an array called W to hold the indices of those nodes that have been encountered, and nextWIdx to hold the index of the next empty position in W (this works like a small stack). Finally, w will hold the index of the node currently being examined. If we call ShortestPath(AdjacencyList[], 6, 1, 5) let's trace what happens. After initializing all the variables and doing the setup they look like figure 8.

In the while loop the first action is to search the list of vertices to find those in the fringe and select the one that is the shortest distance from the starting node v. Nodes 2 and 6 are in the fringe and 2 is only 3 away from 1 while 6 is 5 away so node 2 will be selected. Now we must do three things with node 2: (1) Add it to the W array, (2) change its status in the status array to "intree", and (3) mark all nodes in the status array, which are adjacent to node 2, as "fringe." And finally, (4) we check all nodes adjacent to the current node n (node 2 in this first iteration), calculate a distance from node 1 to the adjacent nodes via node 2. If this distance is less than the given shortest distance in the ShortestDist array then this distance is substituted. We know the shortest distance to node 2 is 3 and that node 2 has nodes 3 and 6 adjacent to it. The distance from node 1 to node 2 is 3 and from node 2 to node 3 is 7 (taken from the adjacency list), so we can calculate a distance from node 1 to node 3 as 3 + 7 = 10. Since 10 is considerably less than MAXINT we set the ShortestDist to node 3 as 10. In the same manner we can calculate a distance to node 6 via node 2 as 3 + 10 = 13. This distance, 13, however is longer than the current distance, 5, so we don't change this distance in the ShortestDist array. This concludes the first iteration of the main while loop and the arrays and variables look like figure 9.
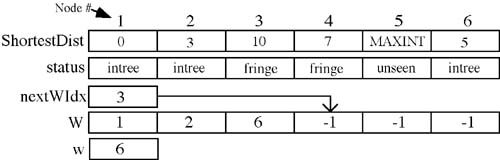
Now we repeat this procedure. In the second iteration nodes 3 and 6 are in the fringe. Since node 6 is closer to node 1 it will be chosen as n for this iteration. Nodes 3 and 4 are adjacent to 6. Shortest distances to these will be calculated. The distance 1-6-3 = 13 which is not shorter than 1-2-3 so that distance in ShortestDist is not updated. The distance 1-6-4 = 7, however is shorter than MAXINT so it is entered as the shortest distance to node 4. After performing all the checks and updates for the second iteration the arrays and variables look like figure 10.
Again we repeat the procedure, this time selecting node 4 from those in the fringe as closest to node 1. With node 4 we add node 5 to the fringe. After all the checks and updates for the third iteration the arrays and variables look like figure 11. Notice that the distance to node 5 (the destination node) at this point is given as 13 (using path 1-6-4-5).
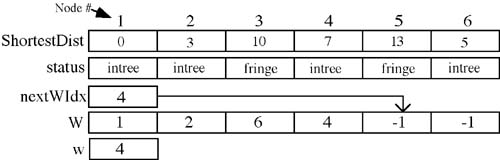
In the fourth iteration node 3 is closest, of those in the fringe, to node 1, with a distance of 10 so it will be added to W. The checks of shortest distance at the end of this iteration will find that node 3 is adjacent to node 5. The distance along the path 1-2-3-5 is calculated as 11. Since this is shorter than the current distance of 13 the new value will be substituted. At the end of the fourth iteration the arrays and variables look like figure 12.
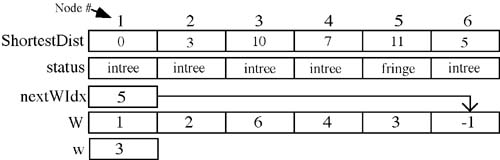
In the fifth and final iteration node 5 will be selected since it is the only one left in the fringe. It's only link is to node 6, but the path to node 6 via node 5 is 16 (11 + 5) which is not shorter than the current distance of 5. After this iteration we see that nextWIdx has been incremented beyond the limits of the array W so the while loop will terminate with the arrays and variables looking like figure 13.
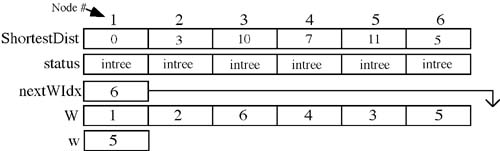
We can now check the array, ShortestDist, for node 5 and return the distance of 11 to the calling function. Notice that the array ShortestDist now contains the shortest path distance to any of the nodes in the graph from the starting node v. See the link below the code for an animation of Dijkstra's algorithm.
#define MAXVERTICES 6 /* only for this example */
#define MAXLINKS 5 /* only for this example */
#define Minimum(X,Y) ((X) < (Y)) ? (X) : (Y)
enum StatusType {intree, fringe, unseen} StatusType;
// See the Code Vault for a full implementation of this algorithm
//-------------------------------------------
// ShortestPath()
//
// Find shortest path from node v to
// node w using Dijkstra's shortest
// path algorithm.
// Returns total number of units in shortest
// path
//-------------------------------------------
int ShortestPath(Node AdjacencyList[], int n, int v, int w)
{
// AdjacencyList -- adjacency list of nodes in graph
// n -- number of nodes in the graph (6)
// v -- number of the starting vertex (1..6)
// w -- number of the destination vertex (1..6)
int MinDistance;
int ShortestDist[MAXVERTICES];
int W[MAXVERTICES];
int nextWIdx = 0;
int i;
int wNode; // Index of node being considered
int tempIdx; // Temporary use index
StatusType status[MAXVERTICES];
// -------------------- INITIALIZATION SECTION --------------------
for(i = 0; i < MAXVERTICES; i++)
{
W[i] = -1; // Init W to empty
ShortestDist[i] = MAXINT; // Init shortest dists to infinity
status[i] = unseen; // Init all nodes to unseen
}
// ------------------------ SETUP SECTION -------------------------
W[nextWIdx] = v; // Add first node to W
nextWIdx++; // Increment index into W
ShortestDist[v-1] = 0; // Set shortest dist from v to v
status[v-1] = intree; // Set status of v in W
// Set shortest distance and status from v to all nodes adjacent to it
for(i = 0; i < MAXLINKS; i++)
{
ShortestDist[AdjacencyList[v-1].links[i].link - 1] =
AdjacencyList[v-1].links[i].weight;
status[AdjacencyList[v-1].links[i].link - 1] = fringe;
}
// ---------------------- MAIN lOOP SECTION -----------------------
// Repeatedly enlarge W until it includes all vertices in the graph
while(nextWIdx < MAXVERTICES)
{
// Find the vertex n in V - W at the minimum distance from v
MinDistance = MAXINT;
for(i = 0; i < MAXVERTICES; i++)
{
if(status[i] == fringe)
{
if(ShortestDist[i] < MinDistance)
{
MinDistance = ShortestDist[i];
wNode = i + 1; // Convert index to node number
}
}
}
// Add w to W
W[nextWIdx] = wNode;
status[wNode - 1] = intree;
nextWIdx++;
// Update the shortest distances to vertices in V - W
for(i = 0; i < MAXLINKS; i++)
{
tempIdx = AdjacencyList[wNode -1].links[i].link - 1;
ShortestDist[tempIdx] = Minimum(ShortestDist[tempIdx],
ShortestDist[wNode - 1] + AdjacencyList[wNode - 1].links[i].weight);
status[tempIdx] = fringe;
}
} // End while
return(ShortestDist[w - 1]);
}