Operators

Operator - A special symbol which represents a process or operation to be performed.

There are a number of different types of operators in the C/C++ language. The tables below summarize those operators.

Math Operators



Relational Operators

These operators are used in conditional statements for if, while, and do-while statements.
==   Is equal to - Determine if two values are equal in conditional statements. Use with caution if the values are float or double.
!=   Not equal - Determine if two values are not equal in conditional statements. Use with caution if the values are float or double.
<   Less than - Determine if one value is less than another value in conditional statements. Use with caution if the values are float or double.
>   Greater than - Determine if one value is greater than another value in conditional statements. Use with caution if the values are float or double.
<=   Less than or equal - Determine if one value is less than or equal to another value in conditional statements. Use with caution if the values are float or double.
>=   Greater than or equal - Determine if one value is greater than or equal to another value in conditional statements. Use with caution if the values are float or double.


Logical Operators

These operators are used in conditional statements to perform logical combinations of more than one conditional (&& and ||) or to invert the result of a conditional (!).
&&   Logical AND - Perform a logical AND operation on two conditionals. If either conditional is false the entire statement is false.
||   Logical OR - Perform a logical OR operation on two conditionals. If either conditional is true the entire statement is true.
!   Logical NOT - Perform a logical NOT operation on a single conditional. This inverts the result of the conditional. If the conditional is true the logical NOT operator makes it false.


Combined Assignment Operators

Obviously Kernighan and Ritchie thought this short cut would be handy. If you have simple math calculations like: You can combine these operations using the combined assignment operators defined below. The place you will see these used most often is in the increment/decrement part of a for loop or when the loop counter is updated in a while or do-while loop. These operators are frequently used with integer variables. They are rarely or never used with float or double variables.
+=   Add and assign - The statement X = X + 1; can be written as X += 1; This sets X to the value of X plus 1.
-=   Subtract and assign - The statement X = X - 2; can be written as X -= 2; This sets X to the value of X minus 2.
*=   Multiply and assign - The statement X = X * 4; can be written as X *= 4; This sets X to the value of X time 4.
/=   Divide and assign - The statement X = X / 2; can be written as X /= 2; This sets X to the value of X divided by 2.
%=   Mod divide and assign - The statement X = X % 2; can be written as X %= 2; This sets X to the remainder of X divided by 2.


Increment/Decrement Operators

These operators are used with integer variables only. These you will see most often in the increment/decrement part of a for loop or when the loop counter is updated in a while or do-while loop.
++   Pre-increment (++X) - Increment the variable value then use it.
++   Post-increment (X++) - Use the current value of the variable then increment it.
--   Pre-decrement (--X) - Decrement the variable value then use it.
--   Post-increment (X--) - Use the current value of the variable then decrement it.
If you are just incrementing or decrementing an integer variable being used as a counter it really doesn't matter whether you pre- or post- increment/decrement. If you are using the value in a math function it does make a difference. Look at the examples below:




Bitwise Operators

We have a number of operators that act directly on the bits in a byte of memory. These are used exclusively with integer variables. See the notes below the table for a detailed discussion of using bitwise operators.
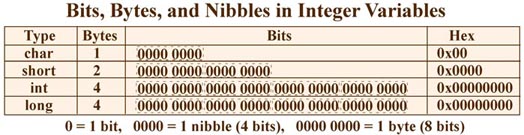
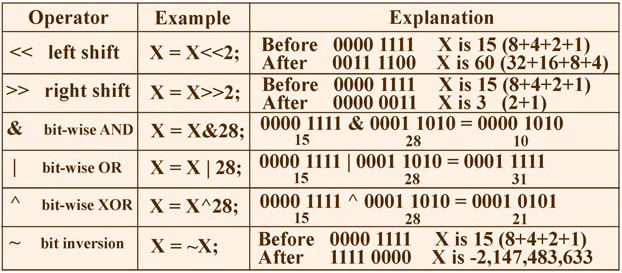
<<   Left bit shift - Shift all bits in the variable to the left. This has the effect of multiplying the value by 2.
>>   Right bit shift - Shift all bits in the variable to the right. This has the effect of dividing the value by 2.
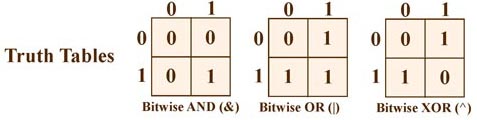
&   Bit-wise AND - Perform a bit-wise AND on the corresponding bits in two integer variables or values.
|   Bit-wise OR - Perform a bit-wise OR on the corresponding bits in two integer variables or values.
^   Bit-wise exclusive OR - Perform a bit-wise XOR (Exclusive OR) on the corresponding bits in two integer variables or values.
~   Bit inversion - Invert all bits in an integer variable. All 1's become zero and all 0's become ones.
These operators are a little more complicated and to understand them you need to understand the structure, in memory, of the char, short, int, and long data types. The table below shows the number of bytes in each of those data types, the way the bits look in memory, and how this value is represented in code in hexadecimal notation.




Numbers that can be represented in one nibble (4 bits) range from zero to fifteen. In binary notation this is 0000 to 1111. In hexadecimal notation this is 0x0 to 0xF.




Numeric Representation

Suppose you have the integer value 15. In decimal (base-10) notation you are accustomed to thinking of this number as five ones plus one ten. For larger numbers you are familiar with the hundreds, thousands, ten-thousands, and so on places. The least significant digit (the one on the right) is the base raised to the zero power (which is always one regardless of the base). The digit in this position is multiplied by the base raised to this power. The next digit over (in the tens position) is miltiplied by the base raised to the first power (which is always just the base). The next digit to the left is the hundreds which is the base raised to the second power.

The same type of notation can be applied to numbers in other bases. The least significant digit is multiplied by the base raised to the zero power. The next digit to the left is multiplied by the base raised to the first power. The next digit to the left is multiplied by the base raised to the second power, and so on.

In computer science the two most used bases are Binary (base-2) and Hexadecimal (base-16). The table below shows how the number 15 is written in decimal, binary, and hexadecimal. The binary number actually shows the layout of the bits in an integer number. The hexadecimal is just a shorthand notation of the bit layout.




Truth Tables

To understand how the bitwise operators work on the bits on variable values you must understand how the bitwise AND, OR, and XOR (exclusive OR) work. This can be diagrammed using what are called truth tables as shown below. For example, in the truth table for bitwise AND: 0 & 0 equals 0, 0 & 1 equals 0, 1 & 0 equals 0. Only 1 & 1 equals 1. You get 1 only if both bits are 1. For the bitwise OR you get 1 if either of the bits are 1. For the bitwise XOR you get 1 only if one of the bits is 1 and the other is 0.




Examples Using Bitwise Operators

Now that you understand the bit layout of integer type variables and the truth tables for the bitwise operators you should have not trouble in understanding what is happening in each of the examples in the table below.

           Given: int X = 15;





Notice that when bits are shifted left or right beyond the limits of the variable size they are lost. Old time programmers like to say they have"fallen off into the bit bucket". In the last example, remember that X is a 4-byte integer. In the diagram only the least significant byte is shown. All bits to the left of this byte will be inverted to ones. Since the most significant bit (the one on the far left) is the sign bit this number representation now becomes negative.

More Combined Assignment Operators

All of the bitwise operators can also be used in combined assignment operators. Note that there is no ~= operator.
<<=   Left shift and assign
>>=   Right shift and assign
&=   AND and assign
|=   OR and assign
^=   XOR and assign

Examples using bitwise combined assignment operators.
X <<<=2;   Set X equal to X bit shifted left by 2 places.
X >>=4;   Set X equal to X bit shifted right by 4 places
X &=18;   Set X equal to X bit ANDed with 18
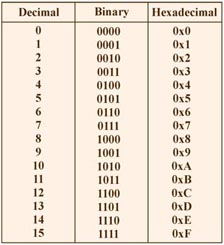
X &=0x12;   Set X equal to X bit ANDed with hex 12 (decimal 18)
X |=7;   Set X equal to X bit Ored with 7
X ^=2;   Set X equal to X bit XORed with 2