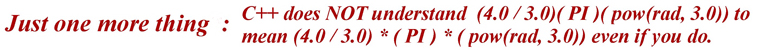Do the Math!

Math Operators


Setting values with the equal (=) operator


Values are stored in variables using the = (equal) operator.
This is not going too fast for you is it? ;-)

Examples of using the math operators

Below are some simple examples using the math operators. Most of this should be easy to understand.

Math Operations Using Decimals Math Operations Using Integers


In these, remember you are doing integer division.
16 divided by 3 gives 5 with a remainder of 1.
16 divided by 2 gives 8 with a remainder of 0.

Precedence

Take a look at the math formula below:


If you expected the answer to be 3.0 you may be surprised to find that answer now holds the value 4.0 instead of 3.0 because of operator Precedence. In C++ math operations multiplication and division are always done first moving from left to right in the equation. Next addition and subtraction are done moving from left to right in the equation.

There is a way around this problem. The answer is to use parentheses. Math operations always follow precedence, but they work from the innermost set of parentheses outward. For example, if the formula given in the above example had been written as:

	
		answer = ((x + y) * 3.0 / 4.0) - 1.5;
The order of calculation would have been as follows: Always use parentheses liberally in math formulas to ensure that the calculations will be performed in the order in which you intended.

The Increment (++) and Decrement (--) operators

Frequently, when you are working with integer variables (short, int, long) you may need to increment (sometimes called "plus-plus") or decrement (sometimes called "minus-minus") a value by one. This is especially useful when you are counting something. The increment (++) and decrement (--) operators do just that.


BTW: The name of our programming language (C++ pronounced "see-plus-plus") got its
name from the increment operator. Bjarne Stroustrup, the developer of C++, meant for it
to be an "increment" on the C programming language.

Data Types in Math Operations

Integer and real numerical values are stored differently in memory and there are actually different mathematical operations to handle the two types. If you include both integer and real variables or numerical literals (the actual numbers) in a line of code, when the math operation is performed all values will be automatically transformed into the greater precision form unless you explicitly specify another form.

The automatic transformation of numerical values to a greater percision form for calculations is called Type Coercion. If you explicitly transform a numerical value into another form it is called Type Casting.




Assume in your code you had declared two variables: an int variable called someInt and a double variable called someDouble.

	int someInt;
	double someDouble;
Suppose, without really thinking, you tried to set someDouble to the literal value 12 which, without a decimal point the computer would take to mean the integer value 12. And, suppose you tried to set someInt to the literal value 4.8, which the computer would take to mean a double value. But, you cannot store a decimal value in an integer variable. 
	someDouble = 12;
	someInt = 4.8;
In these examples we would see automatic type conversion (Type Coercion) occurring. The integer 12 is converted to the double value 12.0 and then stored in the double variable someDouble. The double value 4.8 will be truncated, i.e. the fractional part will be dropped and the value converted to the integer value 4 and then stored in the int variable someInt.

Now look at the other examples of Type Coercion below: 
	someDouble = 3 * someInt + 2;    
	someInt = 5.2 / someDouble + 1.5;
In the first expression (3 * someInt + 2) because all three values are given as integers then integer multiplication and addition will be performed (3 * 4 + 2) to give the integer result of 14 which will then be type coerced to the double value 14.0 before storing in someDouble.

In the second expression (5.2 / someDouble + 1.5) because all three values are given as doubles the double division and addition will be performed (5.2 / 14.0 + 1.5; remember we just changed the value of someDouble from 12.0 to 14.0) to give the double result of 1.871428571429 which will then be type coerced to the integer value of 1 before storing in someInt.

While this type coercion is automatic you can also explicitly make these conversions using Type Casting as shown in the two lines of code below. 
	// Explicit type casting
	someDouble = (float)(3 * someInt + 2); // Result (integer 14) cast to 14.0
	someInt = (int)(5.2 / someDouble + 1.5);  // Result (real 1.8714) is cast to 1
Frequently you will have expressions that are of mixed type, that is you will have both integer and real values mixed. In these cases all values in the mathematical calculation will be automatically coerced to the higher precision format, the calculation performed, then the result coerced to the appropriate data type for the variable where the result is to be stored. 
	// Mixed type expressions
	anotherDouble = someInt * someDouble; // Result is coerced to double
	anotherInt = someInt * someDouble; // Result is coerced to int
In the first expression above the value stored in someInt is first coerced to a double then multiplied by the value stored in someDouble before the result is then stored in the double variable anotherDouble.

In the second expression, again the value stored in someInt is first coerced to a double then multiplied by the value stored in someDouble before the result is then coerced to an integer before being stored in the int variable anotherInt.

WARNING - Be careful in situations like this. 
	int sum = 60;
	int count = 80;
	float average;
You declare two int variables and store values in them. Now you perform a division of sum by count. 
	average = sum / count;
The result of this calculation stores the value 0 in average. Why is this? Because both sum and count are int variables so an integer division is performed which, in this case, gives zero (60 / 80 = 0 with a remainder of 60). To get the correct value you would need to type cast both values to float before performing the calculation. 
 
	average = (float)sum / (float)count;
Now having type cast the integer values in both sum and count to float values the correct result (.75) will be calculated and stored in average.

The Math Library

The C and C++ programming languages have a large collection of utility functions built into the language which you can access by including header files in your code using the #include preprocessor directive. One of the most useful of these for performing math calculations is the math library.

To access all of these functions you must include the following line at the top of the source file where you want to use the math functions.

#include<math.h>

The above line is standard C syntax. You may use this or the standard C++ syntax form below:

#include<math.>
using namespace std;

Below are listed all of the functions found in math.h. Note that the last two listed (finding the absolute value of an int and a long) are found in the header file stdlib (Standard Library) and so you will need to used #include<stdio.h> or #include<cstdio> and using namespace std;




In all of these function angles are given in radians. To convert between radians and degrees use the following conversion formulas:

Angle in Radians = Degrees * 0.0174532925;
Angle in Degrees = Radians * 57.2957795;

Programming Examples using the Math Library

Below are some examples using the math library functions.




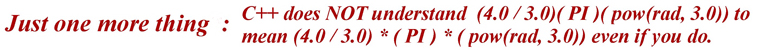
Formatted Output

When you want to print the results of a mathematical calculation you usually want to have some control over how the output is formatted. Below are some of the commands you can include in a cout command to control how numerical values are formatted.




Below are some examples of using these format specifiers.