| Purpose: | Locate a node containing a specified key in a binary tree. |
| Brief: |
Set a pointer to the root of the tree. If the search key is found
in this node return a pointer to it (or a specified data item found
in the node). If not found then set the pointer to the node's left child
if the search key is less than this node's key or to the right child
if the search key is greater than this node's key. Repeat this
until the search key is found or until the pointer becomes NULL. |
|
Cases: |
(1) Tree is empty, nothing to search (2) Search key is found (3) Search key is not found |
|
Typical Function Prototypes: |
In C TreeNode *Search(Keytype searchKey); ReturnType Search(Keytype searchKey); In C++ TreeNode *TreeClass::Search(Keytype searchKey); ReturnType TreeClass::Search(Keytype searchKey); |
| Algorithm: |
If root == Null return NULL Else set a temp pointer = root of the tree Loop while (temp NOT null) AND (key not found) If search key == temp->key Search node found so set FOUND flag to true Else If search key < temp->key temp = temp->left Else temp = temp->right end Loop If temp == NULL return appropriate value to signal search failed else do required action for found item |
|
Example: |
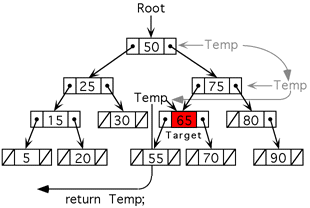
In the example below the search key is 65. The pointer temp is set pointing to root The key is not found so temp is moved to the right (65 > 50) Again the key is not found so temp is moved to the left (65 < 75) On the third attempt the key is found so the pointer to this node is returned. |

| Purpose: | Insert a new node into a binary tree. |
| Brief: |
First search for the place to insert the new node. Set a temp pointer = root, and a back pointer == NULL. Set back = temp. If the key in the new node is less than the key in this node set temp = temp->left else set temp = temp->right. Repeat until temp is NULL. Second insert the new node on the correct side of the parent Back will point to the parent of the new node. Attach new node to the left or right of the parent based on a comparison of the new node's key with the parent's key. |
|
Cases: |
(1) Tree is empty, insert new node as first node in a new tree. (2) Insert new node as a leaf of a parent node. |
|
Typical Function Prototypes: |
In C void Insert(TreeNode *newNode); void Insert(list of data items for a TreeNode); In C++ void TreeClass::Insert(TreeNode *newNode); void TreeClass::Insert(list of data items for a TreeNode); Any of these could also return a boolean value to indicate a successful insertion into the tree. |
| Algorithm: |
Set temp pointer = root, set back pointer = NULL Loop while (temp NOT= NULL) set back = temp If newNode->key < temp->key set temp = temp->left else set temp = temp->right end loop Insert the newNode If back == NULL set root = newNode (first in tree) Else if newNode->key < back->key back->left = newNode Else back->right = newNode |
|
Example: |
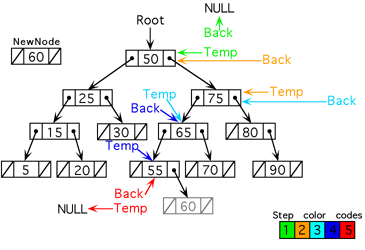
In the example below the new node key is 60. The pointer temp is set pointing to root(green) The pointer back is set pointing to null(green) Temp is moved to the right (60 > 50) with back following (yellow) Temp is moved to the left (60 < 75) with back following (cyan) Temp is moved to the left (60 < 65) with back following (blue) Temp is moved to the right (60 > 50) with back following (red) On this last move temp becomes NULL. Since (60 > 50) the new node is attached on the right side. |
| Purpose: | Delete a node from a binary tree. |
| Brief: |
First find the node to delete. Set a temp pointer = root, set a back pointer = NULL. Advance back to temp. If the search key is less than the key in this node set temp = temp->left else set temp = temp->right. Repeat until the node to delete is found or until temp is NULL. Determine if the node to delete has 0, 1 or 2 children and follow appropriate tree restructuring for that case to remove the node to delete from the tree. Free the deleted node and return the head of the tree. |
|
Cases: |
(1) Tree is empty, nothing to delete. (2) Node to delete was not found. (3) Node to delete has no children. (4) Node to delete has only 1 child on the left (5) Node to delete has only 1 child on the right (6) Node to delete has 2 children. |
|
Typical Function Prototypes: |
In C void Delete(Datatype key); In C++ void TreeClass::Delete(Datatype key); Any of these could also return a boolean value to indicate a successful insertion into the tree. |
|
Algorithm
|
If root is NULL return NULL (Case 1) Set a temp pointer = root, set back pointer == NULL Find position of node to be deleted Loop while (temp NOT=NULL) AND (search key != temp->key) back = temp if (search key < temp->key) set temp = temp->left else set temp = temp->right If (temp == NULL) search key was not found (Case 2) return Else if (temp==root) (deleting root node) set delNode = temp set delParent = NULL Else (deleting a node other than root) set delNode = temp set delParent = back 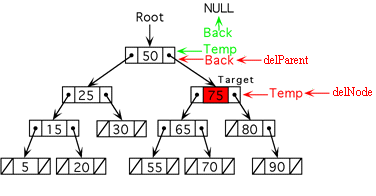
If delNode->right == NULL (Case 3 and/or 4: No children or 1 on left) if delParent == NULL (Deleting the root) set root = delNode->left delete delNode return else (see which side of delParent, delNode is on) if delParent->left == delNode set delParent->left = delNode->left else set delParent->right = delNode->left delete delNode return Else if delNode->left == NULL (Case 5: Only 1 child and it is on right) if delParent == NULL (Deleting the root) set root = delNode->right delete delNode return else (see which side of delParent, delNode is on) if delParent->left == delNode set delParent->left = delNode->right else set delParent->right = delNode->right delete delNode return Else (Case 6: Two children) Find replacement node, i.e. The one with the largest value in the left subtree, but less than the node to be deleted. This will be the right- most node in the left subtree of the node to be deleted. Set temp = delNode->left Set back = delNode while temp->right != NULL back = temp temp = temp->right Copy replacement values from node pointed to by temp into node pointed to by delNode Remove the replacement node (a leaf) from the tree If back == delNode (the first node on the left had no right child) set back->left = temp->left Else set back->right = temp->left delete temp return   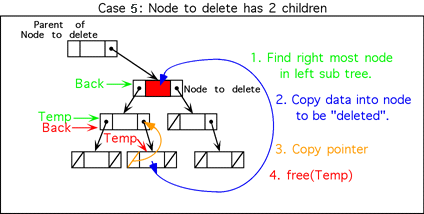 |
| Purpose: | Visit each node in a binary tree. |
| Brief: |
Begin by calling the function and passing in the root. This
will require a separate function if implemented in a class.
If the pointer passed in is not NULL (base case) make a
recursive call to the left, then make a recursive call to
the right. If something is done with the pointer passed
into the function before the recursive calls this is called
a Pre-Order traversal. If something is done with the
pointer between the calls to left and right this is called
an In Order traversal. If something is done with the
pointer after both recursive calls this is called a Post
Order traversal. |
|
Cases: |
Not applicable for this function. |
|
Typical Function Prototypes: |
In C void traverse(TreeNode *rt); In C++ void TreeClass::doTraverse(); // Public function to start the traversal void TreeClass::traverse(TreeNode *rt); // Private function to do the traversal |
| Algorithm: |
If root == Null return Recursively call function with root->left Do something with root Recursively call function with root->right |
|
Example: |
In the example below all data in the tree is printed. A call is made to the function printTree() which is a public function in TreeClass. It makes the first recursive call to printAll() passing in the root. There is another private function called printOne() that takes a pointer to a TreeNode and prints all data in that node. |
// Public function to begin traversal by calling
// the private function and passing in the root
// which is also private.
void TreeClass::printTree()
{
printAll(root); // Make call to private function
}
// Private function to perform in order traversal
// and print all data in the tree
void TreeClass::printAll(TreeNode *rt)
{
if(rt != NULL) // Base case
{
printAll(rt->left); // Recursive call to the left
printOne(rt); // Print data in this node
printAll(rt->right); // Recursive call to the right
}
}
// Function to print all data in one node
void TreeClass::printOne(TreeNode *node)
{
// Code to print all fields in the node
// is placed here.
}
|