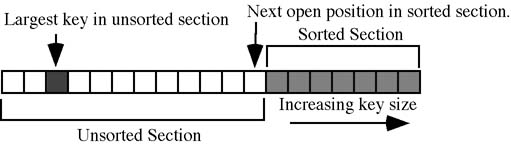
All Priority Queue Sorting is based on arranging the data structures into a priority queue using the keys. Selection Sort divides the array of structures into a sorted and an unsorted section and repeatedly removes the record with the largest key from the unsorted section and moves it to the front of the sorted section.

/***************************************/
/* SelectSort() */
/* */
/* Sort records on integer key using */
/* a selection sort. */
/***************************************/
void SelectSort(StructType DataArray[], int count)
{
int NextIdx; /* Next open position in sorted section */
int LargestKey; /* INdex of largest key in unsorted section */
int i;
StructType temp;
NextIdx = count - 1;
while(NextIdx > 0)
{
LargestKey = NextIdx; /* Initialize the search by assuming the */
/* entry in the next open position in the */
/* sorted section has the largest key. */
/* Find next largest key in unsorted section */
for(i=0; i<NextIdx; i++)
if(DataArray[i].key > DataArray[LargestKey].key)
LargestKey = i;
/* Swap the largest key with the one at the top of the Priority Queue */
temp = DataArray[LargestKey];
DataArray[LargestKey] = DataArray[NextIdx];
DataArray[NextIdx] = temp;
/* Set NextIdx to next position up */
NextIdx--;
}
}