Basic Minimal Spanning Tree Algorithm |
|||
| Set a flag in all vertices to "UNSEEN" | |||
| Pick a starting vertex and mark it as "IN TREE" | |||
| Mark all vertices adjacent to the start vertex as "FRINGE" | |||
| Loop while there are vertices in the graph not marked as "IN TREE" | |||
| Find the vertex in the fringe at a minimum distance from ANY vertex already in the tree. | |||
| Add that vertex to the tree and mark it as "IN TREE" | |||
| Add the weight of the edge between those vertices to the running total | |||
| Mark each vertex adjacent to the just added vertex as "FRINGE" | |||
|
Check the distances to all nodes in the fringe from each vertex in the tree and set each ShortestDistance[] to the minimum distance |
|||
| end loop | |||
| Return total weight of all edges in the minimal spanning tree | |||

There are many situations in real life where a minimal spanning tree is needed. Whenever there is a need to connect a set of nodes (such as cities, electrical terminals, computers or factories) by edges (such as roads, wires, telephone lines, etc.) which are weighted (by length, cost, or some other weighting factor) then a minimal spanning tree is the solution.
Prim's algorithm (sometimes credited to Dijkstra as well) begins by selecting an arbitrary starting vertex and "branches out" from that node by choosing a new vertex and edge in each iteration of the tree building process. At each stage of the tree building process the vertices can be thought of as being divided into three distinct categories:
1. Tree vertices--those vertices that have already been added to the tree.
2. Fringe vertices--those not in the tree, but adjacent to some vertex that is.
3. Unseen vertices--all the other vertices.
The basic algorithm for Prim's Minimal Spanning Tree Algorithm is:
Select an arbritrary vertex to start the tree; while (there are vertices left in the fringe) select an edge between a tree vertex and a fringe vertex with minimum weight add the selected edge and the fringe vertex to the tree
This algorithm is an example of a "greedy" algorithm. A greedy algorithm is one that attempts to find an optimal overall solution by making the best possible choices at each step in the algorithm in hopes that these choices will produce a globally optimal solution. In the case of Prim's algorithm at each iteration the algorithm selects a node from the fringe which is closest to one of the nodes already in the tree.
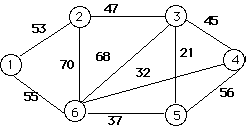
Let's build a minimal spanning tree for the above graph using node 1 as the starting node. Inserting node 1 in the tree gives the following arrangement.


ShortestDist is the shortest distance from a node in the tree to the one in the fringe. MAXINT is a large constant used to indicate that nodes 3, 4, and 5 cannot be reached by any node in the tree. The array status holds an enumerated data type value indicating whether each node has been added to the tree (intree), or is adjacent to a node that is in the tree (fringe), or not (unseen). The integer nextTreetIdx is the index in the Tree array where the next node index will be stored. The integer w is the node currently being added to the tree. After this starting step node 1 has been added to the tree, nodes 2 and 6 are in the fringe, and nodes 3, 4, and 5 are unseen. In the next iteration node 2 will be added to the tree because 53 is less than 55. The results gives the following:


Now the tree consists of nodes 1 and 2. Nodes 3 (adjacent to 2) and 6 (adjacent to 1 and 2) are in the fringe and nodes 4 and 5 are still unseen. The next node to be added to the tree will be node 3 since it is closest of any of the nodes in the fringe to any of the nodes in the tree. After the next iteration the tree diagram looks like this:


Now we have three nodes in the tree (1, 2, and 3). Since nodes 4 and 5 are both adjacent to node 3 we no longer have any nodes that are unseen. In the next iteration we will select node 5 to add to the tree since it is closer to node 3, which is in the tree, than any other node in the fringe is to any node in the tree. After the next iteration the tree diagram looks like this:


There are now only two nodes left in the fringe. Node 6 is 55, 70, 68, and 37 from nodes 1, 2, 3, and 5 respectively. Node 4 is 45 and 56 from nodes 3 and 5. Note that the shortest distance to node 6 has changed to 37 (the distance from node 5). Since this is the shortest distance at this point node 6 is added next. The results gives:


The only remaining node to be added to the tree is node 4. It is 45, 56, and 32 from nodes 3, 5, and 6 respectively. The shortest distance is 32 from node 6 When it is added we have the completed tree.


At this point there are no nodes remaining from the graph that have not been added to the tree. How can we implement this approach to solving the problem of Prim's algorithm? To keep things simple we will implement all of our graph as an adjacency matrix. A 2-D array will do the trick, thus: int adjMatrix[6][6]. A diagram of the matrix representing the graph is shown below.

Here is a more detailed pseudocode algorithm.
#define MAXVERTICES 6 /* only for this example */
#define Minimum(X,Y) ((X) < (Y)) ? (X) : (Y)
typdef enum{intree, fringe, unseen} StatusType;
Define a 2-D array of type int.
Read all data from file and build the matrix to represent the graph.
Input start vertex number (v) from user
Call SpanningTree(adjMatrix, MAXVERTICES, v)
int SpanningTree(int adjMatrix[MAXVERTICES][MAXVERTICES], int n, int v)
/*adjMatrix-- adjacency list of nodes in graph */
n -- number of nodes in the graph (MAXVERTICES)
v -- number of the starting vertex (1..MAXVERTICES)
int ShortestDist[MAXVERTICES];
int Tree[MAXVERTICES];
int nextTreeIdx;
int edgeTotal = 0;
StatusType status[MAXVERTICES];
/* -------------------- INITIALIZATION SECTION -------------------- */
Initialize tree array Tree to empty.
Initialize ShortestDist array to all maximum.
Initialize status array to all unseen.
/* --------------------------- SETUP SECTION --------------------------- */
Add node v to Tree array
Set shortest distance from v to v = 0
Set status of v to intree
For each node adjacent to v
Set status to fringe
Set shortest distance to weight of link from v to w
/* ----------------------- MAIN LOOP SECTION ----------------------- */
/* Repeatedly enlarge Tree until it includes all vertices in the graph */
while(there are nodes in the graph not in Tree)
Find node n, among those in the fringe, at the minimum distance from v
where v is any node in the tree
Add node n to Tree array
Set status of node n to intree
Add weight of edge vn to edgeTotal
For each node adjacent to node n
Set status of adjacent node to fringe
Check distances to all nodes in the fringe from each node in the tree
and set each ShortestDistance[] to the minimum distance.
end while
/* ----------------------- REPORT SECTION ----------------------- */
print the tree in the form of node pairs and the weights of the edges joining them.
Also print the sum of all the edge values. A sample printout of this tree
might look like this:
(1, 2) 53
(2, 3) 47
(3, 5) 21
(5, 6) 37
(6, 4) 32
Total weight = 190
end ShortestPath function
//---------------------------------------------------------------
// File: Code302_Graphs.cpp
// Purpose: Demonstration of Minimal Spanning Tree Algorithm in
// a graph.
// Programming Language: C++
// Author: Dr. Rick Coleman
// Date: March, 2002
//---------------------------------------------------------------
#include <iostream.h>
#include <stdio.h> // Included to give access to sscanf()
#include <stdlib.h> // Included to give access to atoi()
#include <fstream.h>
#include <string.h>
#define MAXVERTICES 6
#define Minimum(X,Y) ((X)<(Y))?(X):(Y)
#ifndef MAXINT
#define MAXINT 65536
#endif
enum StatusType {intree, fringe, unseen};
void SpanningTree(int adjMatrix[MAXVERTICES][MAXVERTICES], int n, int v);
bool getNextLine(ifstream inF, char *line, int lineLen);
int main(void)
{
int adjMatrix[MAXVERTICES][MAXVERTICES];
ifstream inFile;
char line[81], townName[32];
int i, num, vStart;
// Try to open the file with the graph data
inFile.open("graph.txt", ifstream::in);
if(!inFile.is_open())
{
// inFile.is_open() returns false if the file could not be found or
// if for some other reason the open failed.
cout << "Unable to open file graph.txt. \nProgram terminating...\n";
return 0;
}
getNextLine(inFile, line, 81);
num = atoi(line);
// Build the adjaceny matrix
for(i=0; i<num; i++)
{
getNextLine(inFile, line, 81);
sscanf(line, "%s %d %d %d %d %d %d", townName, &adjMatrix[i][0],
&adjMatrix[i][1], &adjMatrix[i][2], &adjMatrix[i][3],
&adjMatrix[i][4], &adjMatrix[i][5]);
}
cout << "\n\nEnter starting node number.\n";
cin >> vStart;
SpanningTree(adjMatrix, MAXVERTICES, vStart);
return 0;
}
//-------------------------------------------
// SpanningTree()
//
// Calculate the minimal spanning tree
// using Prim's algorithm.
//-------------------------------------------
void SpanningTree(int adjMatrix[MAXVERTICES][MAXVERTICES], int n, int v)
{
int ShortestDist[MAXVERTICES][2]; // 0 = shortest dist, 1 = from node
StatusType status[MAXVERTICES];
int nextTreeIdx = 0; // Index in Tree where next node number will be stored
int Tree[MAXVERTICES][2]; // Tree being built. 0 = next vertex, 1 = last vertex
int w; // Current selected vertex
int edgeTotal = 0;
int i;
int minDist;
int fromNode = -1;
//---------------- Initialization Section -----------------
for(i=0; i<MAXVERTICES; i++)
{
ShortestDist[i][0] = MAXINT;
ShortestDist[i][1] = -1;
status[i] = unseen;
Tree[i][0] = Tree[i][1] = -1;
}
//------------------- Setup Section -----------------------
Tree[nextTreeIdx][0] = v; // Add node v to Tree
Tree[nextTreeIdx][1] = 0; // This one had no "from" node
nextTreeIdx++;
ShortestDist[v - 1][0] = 0; // Set shortest distanct from v to v = 0
status[v - 1] = intree; // Set status of v to intree
for(i=0; i<MAXVERTICES; i++) // Search for nodes adjacent to v
{
if(adjMatrix[v - 1][i] > 0) // This one is adjacent
{
status[i] = fringe; // Set status to fringe
ShortestDist[i][0] = adjMatrix[v - 1][i]; // Set shortest distance
ShortestDist[i][1] = v; // Save where this is from
}
}
//------------------ Main Loop Section ---------------------
while(nextTreeIdx < MAXVERTICES) // Repeatedly enlarge tree until it includes
{ // all vertices in the graph
// Find node w among those in the fringe at minimum distance from v
// where v is any node in the tree
minDist = MAXINT;
for(i=0; i<MAXVERTICES; i++)
if((ShortestDist[i][0] < minDist) && (status[i] == fringe))
{
minDist = ShortestDist[i][0];
w = i + 1; // Set to node number not index
}
Tree[nextTreeIdx][0] = w; // Add node to tree
Tree[nextTreeIdx][1] = ShortestDist[w - 1][1]; // Save from node
status[w - 1] = intree; // Set status of w to intree
edgeTotal += minDist; // Add distance to running total
for(i=0; i<MAXVERTICES; i++)
{ // For each node adjacent to w
if((adjMatrix[w - 1][i] > 0) && (status[i] == unseen)) // This one is adjacent and not in fringe
status[i] = fringe; // Set this one to in fringe
// Set new minimum distance if appropriate
if((adjMatrix[w - 1][i] > 0) && (status[i] == fringe)) // This one is adjacent and not in fringe
ShortestDist[i][0] = Minimum(ShortestDist[i][0], adjMatrix[w - 1][i]);
if(ShortestDist[i][0] == adjMatrix[w - 1][i])
ShortestDist[i][1] = w; // Set from node
}
nextTreeIdx++;
}
//-------------------- Report Section ---------------------
cout << "\n\nMinimal Spanning Tree:\n";
cout << "----------------------\n";
for(i=1; i<MAXVERTICES; i++)
cout << "(" << Tree[i][1] << " to " << Tree[i][0] << ") dist = " <<
ShortestDist[i][0] << "\n";
cout << "----------------------\n";
cout << "\nTotal distance = " << edgeTotal << "\n";
}
//-------------------------------------------
// GetNextLine()
// Read the next line from the file.
//-------------------------------------------
bool getNextLine(ifstream inF, char *line, int lineLen)
{
int done = false;
while(!done)
{
inF.getline(line, lineLen);
if(inF.good()) // If a line was successfully read
{
if(strlen(line) == 0) // Skip any blank lines
continue;
else if(line[0] == '#') // Skip any comment lines
continue;
else done = true; // Got a valid data line so return with this line
}
else
{
strcpy(line, "");
return false; // Flag end of file with null string
}
} // end while
return true; // Flag successful read
}
Baase, Sara Computer Algorithms: Introduction to Design and Analysis, 2nd ed., Addison- Wesley Publishing Company, 1988