This page was last updated February 21, 2003
Graph Basics
Graph Terms
-
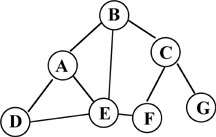
Graph - A collection of nodes (data structures stored in either an array or
a linked arrangement) in which pairs of nodes in the collection are connected by
links known as edges.
-
Vertex - A node in a graph.
-
Edge - A connection between two nodes in graph.
-
Undirected Graph - A graph in which the paths (links) between
vertices go in both directions.
-
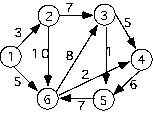
Directed Graph (Digraph) - A graph in which the paths (links) between
vertices go in only one direction. This is indicated in diagrams by drawing the
lines connecting vertices as arrows indicating the direction of movement.
-
Adjacent Vertices - Two vertices are adjacent if there is an edge
connecting them.
-
Path - A list of vertices indicating those that must be visited in order
to get from one vertex to another.
-
Length of a Path - The number of edges from the starting vertex to the
ending vertex.
-
Simple Cycle - A path consisting of three or more distinct vertices that
starts and ends on the same vertex, and visits no vertex more than once except
for the starting/ending vertex, e.g. A--B--C--A.
-
Connected Vertices - Two vertices, in an undirected graph, in which there
is a path between them. A set of vertices (which may not be all the vertices in
a graph) are said to be connected if for any one vertex in the set there is a
path to every other vertex in the set.
-
Connected Components - A subset of connected vertices in a graph
which is not connected to the remainder of vertices. For example: If a
graph contains 6 nodes (A, B, C, D, E, F) and nodes (A, B, C) are connected
as are nodes (D, E, F), but there is no connection between the two subsets,
each is said to be a "connected component" of the graph.
-
Adjacency Set - A way of implementing a graph representation in code.
This consists of a linked list of "graph node" structures representing the
nodes in the graph. Each node contains a pointer to a linked list of "link"
structures. Each link structure then contains a pointer to a another node
to which this node has a link.
-
Adjacency Matrix - A way of implementing a graph representation in code.
This consists of an array of "graph node" structures representing the
nodes in the graph. A two-dimensional array (matrix) is used to store the
links with the rows representing each node in the graph and the columns
representing "links to".
-
Degree of a Vertex - How many other nodes a given vertex
is connected to.
-
Predecessors - In a directed graph a vertex's predecessors are
those nodes from which there is an edge leading to the selected node.
-
In-degree of a node - The number of predecessors a node has.
-
Succesors - In a directed graph a vertex's successors are
those nodes to which there is an edge leading from the selected node.
-
Out-degree of a node - The number of successors a node has.
Graph Symbols
Frequently symbols are used to represent graphs and their components as a sort of
short-hand. The following are the more commonly used symbols.
-
G=(V,E) - Defines a graph as a set of vertices (V) and a set
of edges (E) joining the vertices.
-
e={V1,V2} - Defines a edge in a graph joining
two vertices. If this is an edge in an undirected graph then the order of
V1 and V2 does not matter. If this is an edge in a
directed graph then the vertices form an ordered pair and V1 is
the origin and V2 is the terminus.
-
e
 E - Defines an edge (e)
contained in the set of edges (E).
E - Defines an edge (e)
contained in the set of edges (E).
-
p=v1,v2...vn, (n>=2)
- Defines a path going from v1 to vn as
long as n>=2.
-
p=v1,v2...vn, (v1=vn)
- Defines a cycle going from v1 to vn.
-
T
 S - Subset S of nodes in a graph
is completely contained in set T.
S - Subset S of nodes in a graph
is completely contained in set T.
-
S1
 S2 -
Intersection of S1 and S2, i.e. all s contained
in both S1 and S2.
S2 -
Intersection of S1 and S2, i.e. all s contained
in both S1 and S2.
-
S1
 S2 -
Union of S1 and S2, i.e. all s contained
in either S1 or S2.
S2 -
Union of S1 and S2, i.e. all s contained
in either S1 or S2.
-
Vx={y | (x,y)
 E} -
The set of all vertices (y) such that there is an edge (x,y) contained
in the set of edges (E). This defines the set of edges connected to
a particular node.
E} -
The set of all vertices (y) such that there is an edge (x,y) contained
in the set of edges (E). This defines the set of edges connected to
a particular node.
Graph Representation
There are two primary way of representing graphs in code. These are the Adjacency
Matrix and the Adjacency Set
Adjacency Matrix
In an Adjacency Matrix representation the nodes in a graph are represented as
an array of data structures. The links are then represented in a matrix defined
as a two-dimensional array. Each row in the matrix represents a the node
in the array with the same index. The columns in the row then represent links
to other nodes. For example, suppose we have the following simple graph:
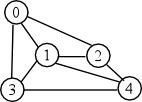
We can define the needed data arrays and structures as:
struct GraphNode
{
// Define data to be stored in each node
};
GraphNode NodeArray[5];
int AdjMatrix[5][5];
To represent the links we would let the rows in AdjMatrix represent each
node with row 0 corresponding to the node store in NodeArray[0] and
representing Node 0 in the diagram. To represent the links from this
node to others (Nodes 1, 2, and 3) in the graph we would set columns 1, 2,
and 3 in of row 0 to 1 and all the other columns to 0. We let the collumn
corresponding to the node itself default to 0. The complete
matrix would look like this:
|
|
0
|
1
|
2
|
3
|
4
|
|
0
|
0
|
1
|
1
|
1
|
0
|
|
1
|
1
|
0
|
1
|
1
|
1
|
|
2
|
1
|
1
|
0
|
0
|
1
|
|
3
|
1
|
1
|
0
|
0
|
1
|
|
4
|
0
|
1
|
1
|
1
|
0
|
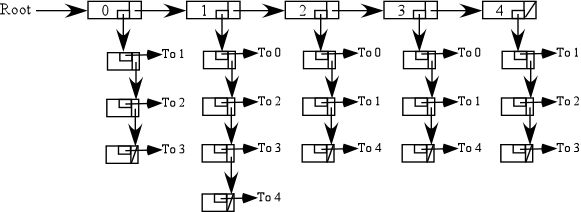
Adjacency Set
In an Adjacency Set representation the nodes in a graph are represented as
a linked list of data structures. The links are then represented as a linked
list of link data structures. Using the same graph as above we can define
appropriate data structures.
struct GraphLink; // Forward declaration so it can be used
// in the next structure
struct GraphNode
{
// Define data to be stored in each node
GraphNode *next;
GraphLink *links;
};
struct GraphLink // Now define the GraphLink structure
{
GraphNode *linkTo;
GraphLink *next;
};
Now the graph would be represented as a linked list of linked lists like this:




 E - Defines an edge (e)
contained in the set of edges (E).
E - Defines an edge (e)
contained in the set of edges (E).
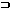 S - Subset S of nodes in a graph
is completely contained in set T.
S - Subset S of nodes in a graph
is completely contained in set T.
 S2 -
Intersection of S1 and S2, i.e. all s contained
in both S1 and S2.
S2 -
Intersection of S1 and S2, i.e. all s contained
in both S1 and S2.
 S2 -
Union of S1 and S2, i.e. all s contained
in either S1 or S2.
S2 -
Union of S1 and S2, i.e. all s contained
in either S1 or S2.
 E} -
The set of all vertices (y) such that there is an edge (x,y) contained
in the set of edges (E). This defines the set of edges connected to
a particular node.
E} -
The set of all vertices (y) such that there is an edge (x,y) contained
in the set of edges (E). This defines the set of edges connected to
a particular node.

