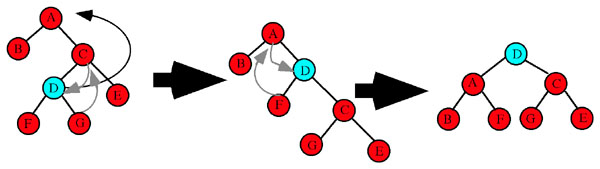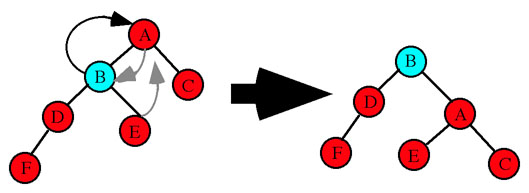
Figure 6: AVL Tree Single Right Rotation
An AVL Tree is one that, by definition, must meet the following criteria:
AVL trees provide a way to keep binary trees close to being balanced all the time. They were developed by two Russian mathematicians Adelson-Velskii, and Landis (thus the name "AVL".)
Each time a node is inserted into an AVL tree a function is called to check the AVL property of the tree and, if require, rebuild the tree to maintain the AVL quality. This will require the shifting of some nodes to reform the tree. As it turns out there are 4 different tree transformations which are required. These tree transformations are called Rotations. They are:
The illustrations below show how these rotations are done:
Single right rotation: Node B is moved up. Node A becomes the right child of Node B and Node E becomes the left child of A (Figure 6). Study carefully the arrangement of the keys in a binary tree and you will see that this new balanced arrangement also maintains the binary tree quality, i.e. all nodes in the left sub-tree have keys less than a given node and all nodes in the right sub-tree have keys greater than a given node.

Single left rotation: Node C is moved up. Node A becomes the left child of Node C and Node D becomes the right child of A (Figure 7).
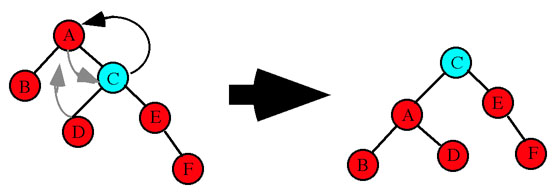
Double right rotation: Node E is moved up. In the first step Node B becomes the left child of Node E and Node F becomes the right child of Node B. In the second step Node E moves up to its final position and Node A becomes the right child of Node E while Node G becomes the left child of Node A (Figure 8).
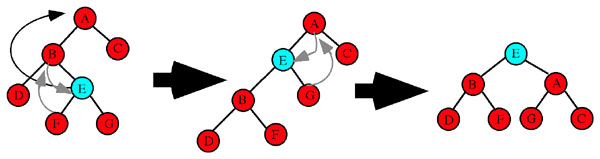
Double left rotation: Node D is moved up. In the first step Node C becomes the right child of Node D and Node G becomes the left child of Node C. In the second step Node D moves up to its final position and Node A becomes the left child of Node D while Node F becomes the right child of Node A (Figure 9).