This page was last updated January 11, 2007

Other Tree Structures

In this section a variety of tree structures, other than the binary tree, will be discussed.

Heap

A Heap is defined as a complete binary tree with key values stored in the nodes in a way that no child node has a key value greater than its' parent. Be careful, and do not confuse the definition of a heap as a tree structure with the area of memory used for dynamic memory allocation which is also called a "heap".

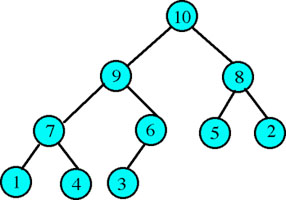
Figure 1 illustrates a heap in which the key values are integers (1...10). Note that no matter which node you consider in this structure all of the child nodes under that node have key values less than its' key value.


Figure 1: A Heap

A Heap, by its structure, can be used as a priority queue. Because of its structure the item with the largest key value (highest priority) will always be at the root of the heap. The Dequeue() function removes this root node, rebuilds the heap so as to maintain the heap quality, and returns the data stored in the root node.

The function used to rebuild the heap is usually called "Reheap()". It works like this:

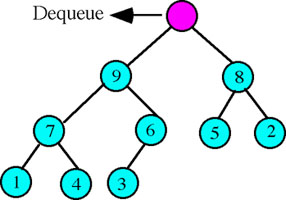
Step 1: Dequeue the root. That is, copy the data in the root node to a temporary storage area (Figure 2).


Figure 2: Dequeue the root

Step 2: Locate the right-most leaf node in the lowest level of the heap and copy the data in this node into the root position then delete this leaf node. Note that doing so will preserve the heap structure as a complete binary tree.


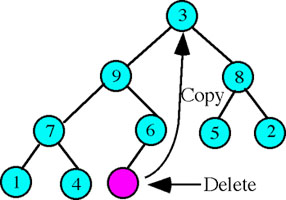
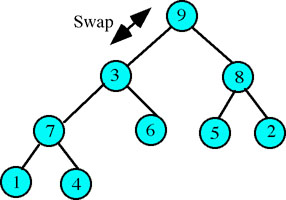
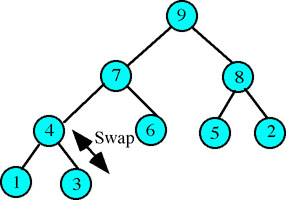
Figure 3: Copy leaf to root then delete leaf.

Step 3: Rebuild the heap so that it again meets the requirement that each node will have a key value greater than any of its' children. This consists of first finding the child node to the root with the greatest key value (the left child in this example) and swapping the data in that node with the data in the root (Figure 4).


Figure 4: Reheap down

Continue this "reheaping" process until the data that was originally moved to the root moves back down to a position where it meets the heap requirements, i.e. all its' child nodes have key values less than it has. This is illustrated in Figure 5.
          
Figure 5: Continue reheaping down.

2-3 Trees

A 2-3 Tree is another attempt to maintain balance in a tree structure. A 2-3 tree meets the following criteria:

  1. All subtrees are kept in perfect balance.
  2. Each node may contain one or two keys and have two or three subtrees.
A 2-3 tree structure is illustrated in Figure 10, below. All leaf nodes are represented by small squares. Non-leaf nodes are represented by rounded rectangles which contain one or two keys (thus one or two sets of data). Note that all the leaf nodes are on the same level, thus the tree is in perfect balance.

To search for a particular node in the tree one uses a modification of the binary tree search. If a node contains only one key the decision to move left or right is the same as in a binary tree. If a node contains two keys the decision to move will be either to the left sub-tree, middle sub-tree, or right sub-tree depending on whether the search key is less than both keys in the node, between the keys, or greater than both keys.

Inserting a node becomes more difficult because the tree must be maintained in perfect balance. In the following diagrams Node M is to be inserted into the 2-3 tree (Figure 10).


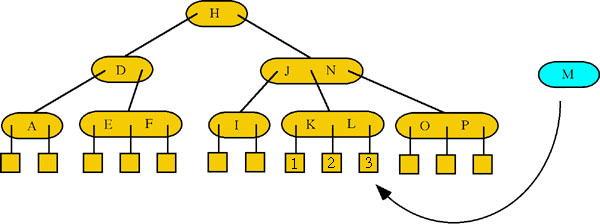
Figure 10: Inserting a node into a 2-3 tree

Step 1: New Node M should go to the right of Node L, but to do so would place three keys in Node KL, which is not allowed. In order to keep all leaf nodes on the same level Node KL is split into two nodes, the leaf nodes arranged appropriately and Node L is now passed up a level (Figure 11).


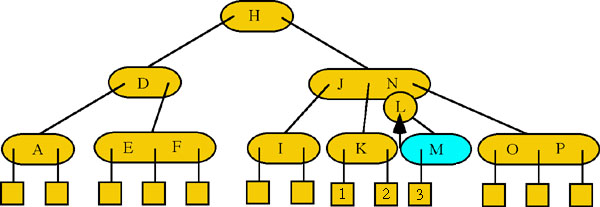
Figure 11: Node KL is split and L passed up

Step 2: If Node L is passed up this will give three keys in the parent node so it is split into Nodes J and N and Node L is again passed up. (Figure 12).


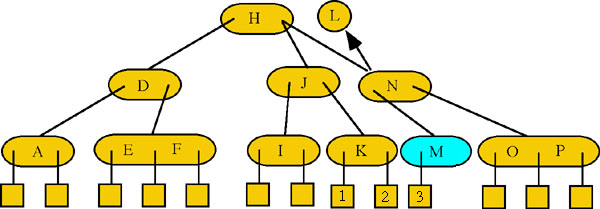
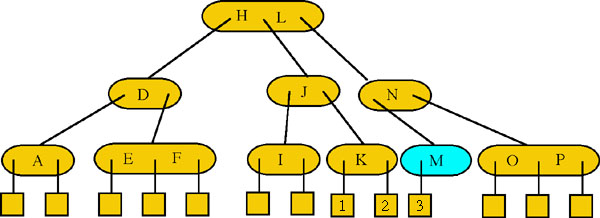
Figure 12: Node JN is split and L passed up

Step 3: Finally node L is inserted into the root node giving it two keys.(Figure 13) Note, that if another node is inserted that results in a node being passed back up to the root then the root would be split with one of the nodes being passed up to become a new root and each leaf would then be moved to one level lower. But, the tree would still maintain a perfect balance.


Figure 13: Node JN is split and L passed up

B-Trees

A B-Tree is a special form of the 2-3 tree in which each node is allowed to have a large number of keys. If we allow B-tree nodes to have between 128 and 256 child nodes then the B-tree is said to be of Order 256.


Figure 14: A B-tree

Given a B-tree of order m, it meets the following criteria:
  1. All internal nodes (that is all except the root and leaves) can have between m/2 and m children. If a node has m children and one more gets added then it will be split into two nodes, each with m/2 children, and the extra node will be passed up just as in the 2-3 tree structure.
  2. The root can have from 2 to m children.
  3. All leaves lie on the same bottom most level.

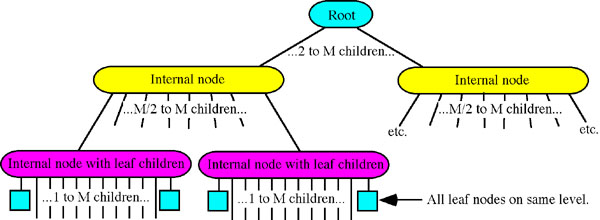
B-trees are primarily used when very large amounts of data are being manipulated such that all the data cannot be kept in memory at one time, but must be stored externally on large capacity hard drives. Then only the keys need be kept in memory with a pointer to where all child nodes are for each parent.


Tries

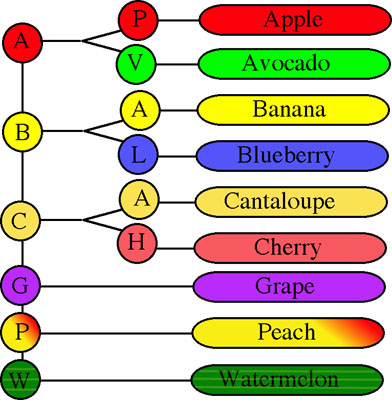
This is a special type of tree structure. The name comes from retrieval, but is pronounced as if it rhymes with "pie" (go figure). Quite simply this is a form of alphabetical organizing of node keys.

Suppose we have the keys Apple, Avocado, Banana, Blueberry, Cantaloupe, Cherry, Grape, Peach, and Watermelon. A Trie structure created from these nodes would look like that shown in Figure 15. There would be a special node containing the key "A" linked to two more special nodes "P" and "V" which in turn would link to the nodes with the keys "Apple" and "Avocado" respectively. As more nodes are added additional special keys are added as needed.


Figure 15: A Trie