Merge Sort

Sort Type: Comparison-Based Sorting / Divide and Conquer Sorting

Algorithm

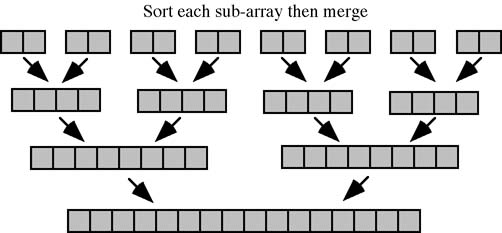
The basic idea behind Divide and Conquer Sorting is to divide the data into two smaller groups, sort these, then combine the two small sorted groups into one larger sorted group. Merge Sort is frequently used to sort very large collections of data stored on external devices. These techniques lend themselves to recursive calls and are frequently used in this way.

1. If the array to be sorted has more than one item in it divide it into two parts.
2. Recursively call MergeSort() to sort the first half-Array.
3. Recursively call MergeSort() to sort the second half-Array.
4. Merge the two half-arrays

   

Sample Code:

/***************************************/
/* MergeSort()                         */
/*                                     */
/* Sort records on integer key using   */
/*  a merge sort.                      */
/***************************************/
void MergeSort(StructType DataArray[], int startIdx, int endIdx)
{
    int        start, end;

    if(startIdx < endIdx)    // If there is more than one item to sort 
    {
        start = startIdx;
        end = startIdx + ((endIdx - startIdx) / 2);
        MergeSort(DataArray, start, end);
        start = end + 1;
        end = endIdx;
        MergeSort(DataArray, start, end);
        Merge(DataArray, startIdx, start - 1, start, end);
    }
}

/***************************************/
/* Merge()                             */
/* Merge the two sections of the array */
/*  using Insertion Sort treating one  */
/*  section as the sorted section and  */
/*  the other as the unsorted section. */
/***************************************/
void Merge(SortData Array1[], int start1, int end1, 
          int start2, int end2)
{
     int          i, j;
     SortData     temp;
     int          NotDone;
     int          Key;

	 for(i=start2; i<=end2; i++)
     {
          Key = Array1[i].key;
          j = i;
          NotDone = (Array1[j-1].key > Key);
          temp = Array1[j]; 
		  while(NotDone)
          {
               // Slide all others to the right 
               Array1[j] = Array1[j-1];
               j--;
               if(j > start1)
                    NotDone = (Array1[j - 1].key > Key);
               else
                    NotDone = FALSE;
          }
          // Put removed record into correct slot
          Array1[j] = temp;
     }
}